Searching for Optimal Per-Coordinate Step-sizes with Multidimensional Backtracking

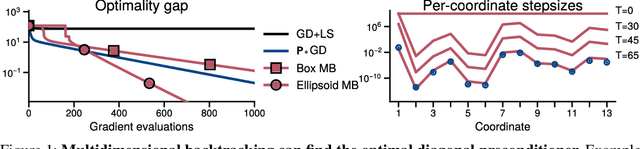
The backtracking line-search is an effective technique to automatically tune the step-size in smooth optimization. It guarantees similar performance to using the theoretically optimal step-size. Many approaches have been developed to instead tune per-coordinate step-sizes, also known as diagonal preconditioners, but none of the existing methods are provably competitive with the optimal per-coordinate stepsizes. We propose multidimensional backtracking, an extension of the backtracking line-search to find good diagonal preconditioners for smooth convex problems. Our key insight is that the gradient with respect to the step-sizes, also known as hypergradients, yields separating hyperplanes that let us search for good preconditioners using cutting-plane methods. As black-box cutting-plane approaches like the ellipsoid method are computationally prohibitive, we develop an efficient algorithm tailored to our setting. Multidimensional backtracking is provably competitive with the best diagonal preconditioner and requires no manual tuning.