New Algorithms for Multiplayer Bandits when Arm Means Vary Among Players

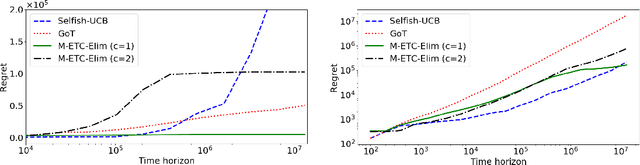
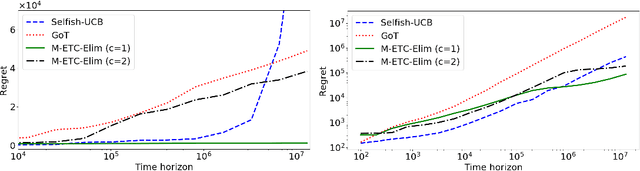
We study multiplayer stochastic multi-armed bandit problems in which the players cannot communicate,and if two or more players pull the same arm, a collision occurs and the involved players receive zero reward.Moreover, we assume each arm has a different mean for each player. Let $T$ denote the number of rounds.An algorithm with regret $O((\log T)^{2+\kappa})$ for any constant $\kappa$ was recently presented by Bistritz and Leshem (NeurIPS 2018), who left the existence of an algorithm with $O(\log T)$ regret as an open question. In this paper, we provide an affirmative answer to this question in the case when there is a unique optimal assignment of players to arms. For the general case we present an algorithm with expected regret $O((\log T)^{1+\kappa})$, for any $\kappa>0$.