Evolving Ranking Functions for Canonical Blow-Ups in Positive Characteristic

Resolution of singularities in positive characteristic remains a long-standing open problem in algebraic geometry. In characteristic zero, the problem was solved by Hironaka in 1964, work for which he was awarded the Fields Medal. Modern proofs proceed by constructing suitable ranking functions, that is, invariants shown to strictly decrease along canonical sequences of blow-ups, ensuring termination. In positive characteristic, however, no such general ranking function is known: Frobenius-specific pathologies, such as the kangaroo phenomenon, can cause classical characteristic-zero invariants to plateau or even temporarily increase, presenting a fundamental obstruction to existing approaches. In this paper we report a sequence of experiments using the evolutionary search model AlphaEvolve, designed to discover candidate ranking functions for a toy canonical blow-up process. Our test benchmarks consist of carefully selected hypersurface singularities in dimension $4$ and characteristic $p=3$, with monic purely inseparable leading term, a regime in which naive order-based invariants often fail. After iteratively refining the experimental design, we obtained a discretized five-component lexicographic ranking function satisfying a bounded-delay descent criterion with zero violations across the benchmark. These experiments in turn motivated our main results: the conjectural delayed ranking functions in characteristic $3$ formulated in two conjectures.

Flow-based Extremal Mathematical Structure Discovery

The discovery of extremal structures in mathematics requires navigating vast and nonconvex landscapes where analytical methods offer little guidance and brute-force search becomes intractable. We introduce FlowBoost, a closed-loop generative framework that learns to discover rare and extremal geometric structures by combining three components: (i) a geometry-aware conditional flow-matching model that learns to sample high-quality configurations, (ii) reward-guided policy optimization with action exploration that directly optimizes the generation process toward the objective while maintaining diversity, and (iii) stochastic local search for both training-data generation and final refinement. Unlike prior open-loop approaches, such as PatternBoost that retrains on filtered discrete samples, or AlphaEvolve which relies on frozen Large Language Models (LLMs) as evolutionary mutation operators, FlowBoost enforces geometric feasibility during sampling, and propagates reward signal directly into the generative model, closing the optimization loop and requiring much smaller training sets and shorter training times, and reducing the required outer-loop iterations by orders of magnitude, while eliminating dependence on LLMs. We demonstrate the framework on four geometric optimization problems: sphere packing in hypercubes, circle packing maximizing sum of radii, the Heilbronn triangle problem, and star discrepancy minimization. In several cases, FlowBoost discovers configurations that match or exceed the best known results. For circle packings, we improve the best known lower bounds, surpassing the LLM-based system AlphaEvolve while using substantially fewer computational resources.

A Note on Small Percolating Sets on Hypercubes via Generative AI

We apply a generative AI pattern-recognition technique called PatternBoost to study bootstrap percolation on hypercubes. With this, we slightly improve the best existing upper bound for the size of percolating subsets of the hypercube.

Reinforcement Learning the Chromatic Symmetric Function

We propose a conjectural counting formula for the coefficients of the chromatic symmetric function of unit interval graphs using reinforcement learning. The formula counts specific disjoint cycle-tuples in the graphs, referred to as Eschers, which satisfy certain concatenation conditions. These conditions are identified by a reinforcement learning model and are independent of the particular unit interval graph, resulting a universal counting expression.

An ML approach to resolution of singularities

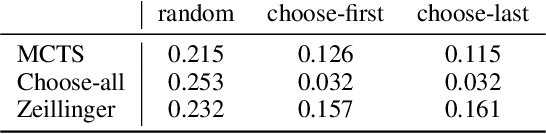
The solution set of a system of polynomial equations typically contains ill-behaved, singular points. Resolution is a fundamental process in geometry in which we replace singular points with smooth points, while keeping the rest of the solution set unchanged. Resolutions are not unique: the usual way to describe them involves repeatedly performing a fundamental operation known as "blowing-up", and the complexity of the resolution highly depends on certain choices. The process can be translated into various versions of a 2-player game, the so-called Hironaka game, and a winning strategy for the first player provides a solution to the resolution problem. In this paper we introduce a new approach to the Hironaka game that uses reinforcement learning agents to find optimal resolutions of singularities. In certain domains, the trained model outperforms state-of-the-art selection heuristics in total number of polynomial additions performed, which provides a proof-of-concept that recent developments in machine learning have the potential to improve performance of algorithms in symbolic computation.