The Common Pile v0.1: An 8TB Dataset of Public Domain and Openly Licensed Text

Large language models (LLMs) are typically trained on enormous quantities of unlicensed text, a practice that has led to scrutiny due to possible intellectual property infringement and ethical concerns. Training LLMs on openly licensed text presents a first step towards addressing these issues, but prior data collection efforts have yielded datasets too small or low-quality to produce performant LLMs. To address this gap, we collect, curate, and release the Common Pile v0.1, an eight terabyte collection of openly licensed text designed for LLM pretraining. The Common Pile comprises content from 30 sources that span diverse domains including research papers, code, books, encyclopedias, educational materials, audio transcripts, and more. Crucially, we validate our efforts by training two 7 billion parameter LLMs on text from the Common Pile: Comma v0.1-1T and Comma v0.1-2T, trained on 1 and 2 trillion tokens respectively. Both models attain competitive performance to LLMs trained on unlicensed text with similar computational budgets, such as Llama 1 and 2 7B. In addition to releasing the Common Pile v0.1 itself, we also release the code used in its creation as well as the training mixture and checkpoints for the Comma v0.1 models.

When AI Co-Scientists Fail: SPOT-a Benchmark for Automated Verification of Scientific Research

Recent advances in large language models (LLMs) have fueled the vision of automated scientific discovery, often called AI Co-Scientists. To date, prior work casts these systems as generative co-authors responsible for crafting hypotheses, synthesizing code, or drafting manuscripts. In this work, we explore a complementary application: using LLMs as verifiers to automate the \textbf{academic verification of scientific manuscripts}. To that end, we introduce SPOT, a dataset of 83 published papers paired with 91 errors significant enough to prompt errata or retraction, cross-validated with actual authors and human annotators. Evaluating state-of-the-art LLMs on SPOT, we find that none surpasses 21.1\% recall or 6.1\% precision (o3 achieves the best scores, with all others near zero). Furthermore, confidence estimates are uniformly low, and across eight independent runs, models rarely rediscover the same errors, undermining their reliability. Finally, qualitative analysis with domain experts reveals that even the strongest models make mistakes resembling student-level misconceptions derived from misunderstandings. These findings highlight the substantial gap between current LLM capabilities and the requirements for dependable AI-assisted academic verification.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Grokking Group Multiplication with Cosets

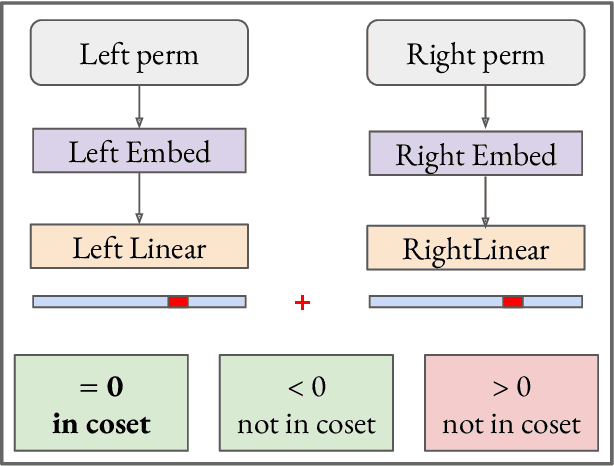
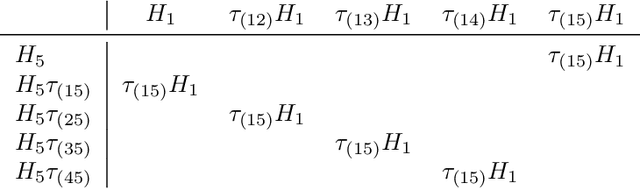
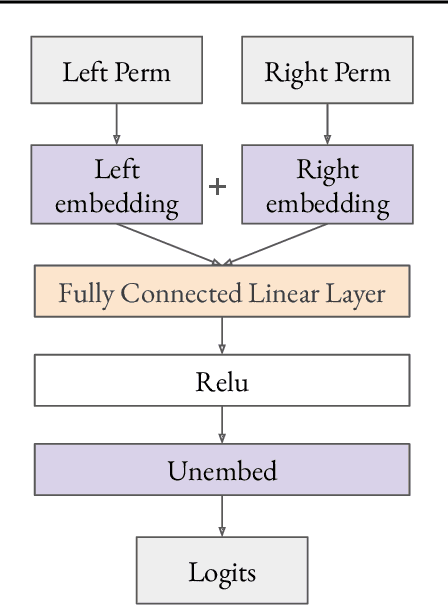
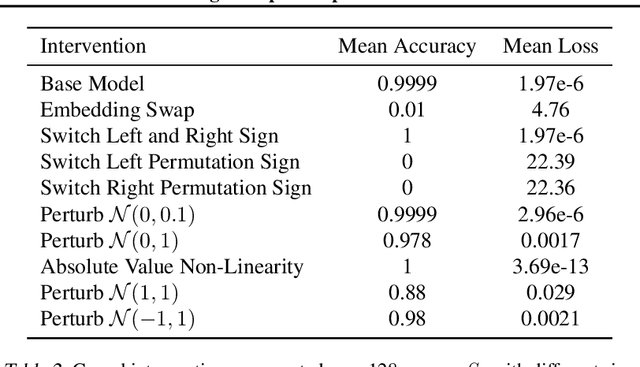
We use the group Fourier transform over the symmetric group $S_n$ to reverse engineer a 1-layer feedforward network that has "grokked" the multiplication of $S_5$ and $S_6$. Each model discovers the true subgroup structure of the full group and converges on circuits that decompose the group multiplication into the multiplication of the group's conjugate subgroups. We demonstrate the value of using the symmetries of the data and models to understand their mechanisms and hold up the ``coset circuit'' that the model uses as a fascinating example of the way neural networks implement computations. We also draw attention to current challenges in conducting mechanistic interpretability research by comparing our work to Chughtai et al. [6] which alleges to find a different algorithm for this same problem.

YaRN: Efficient Context Window Extension of Large Language Models

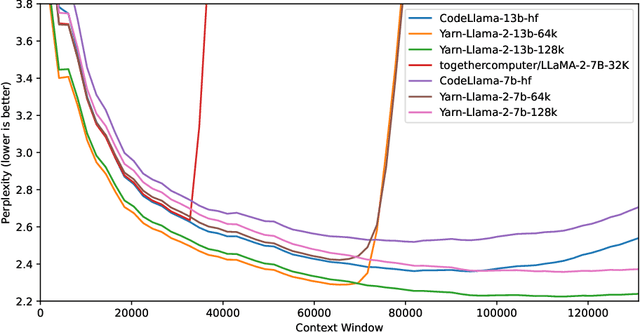
Rotary Position Embeddings (RoPE) have been shown to effectively encode positional information in transformer-based language models. However, these models fail to generalize past the sequence length they were trained on. We present YaRN (Yet another RoPE extensioN method), a compute-efficient method to extend the context window of such models, requiring 10x less tokens and 2.5x less training steps than previous methods. Using YaRN, we show that LLaMA models can effectively utilize and extrapolate to context lengths much longer than their original pre-training would allow, while also surpassing previous the state-of-the-art at context window extension. In addition, we demonstrate that YaRN exhibits the capability to extrapolate beyond the limited context of a fine-tuning dataset. We publish the checkpoints of Llama 2 7B/13B fine-tuned using YaRN with 64k and 128k context windows at https://github.com/jquesnelle/yarn

An ML approach to resolution of singularities

The solution set of a system of polynomial equations typically contains ill-behaved, singular points. Resolution is a fundamental process in geometry in which we replace singular points with smooth points, while keeping the rest of the solution set unchanged. Resolutions are not unique: the usual way to describe them involves repeatedly performing a fundamental operation known as "blowing-up", and the complexity of the resolution highly depends on certain choices. The process can be translated into various versions of a 2-player game, the so-called Hironaka game, and a winning strategy for the first player provides a solution to the resolution problem. In this paper we introduce a new approach to the Hironaka game that uses reinforcement learning agents to find optimal resolutions of singularities. In certain domains, the trained model outperforms state-of-the-art selection heuristics in total number of polynomial additions performed, which provides a proof-of-concept that recent developments in machine learning have the potential to improve performance of algorithms in symbolic computation.

Stay on topic with Classifier-Free Guidance

Classifier-Free Guidance (CFG) has recently emerged in text-to-image generation as a lightweight technique to encourage prompt-adherence in generations. In this work, we demonstrate that CFG can be used broadly as an inference-time technique in pure language modeling. We show that CFG (1) improves the performance of Pythia, GPT-2 and LLaMA-family models across an array of tasks: Q\&A, reasoning, code generation, and machine translation, achieving SOTA on LAMBADA with LLaMA-7B over PaLM-540B; (2) brings improvements equivalent to a model with twice the parameter-count; (3) can stack alongside other inference-time methods like Chain-of-Thought and Self-Consistency, yielding further improvements in difficult tasks; (4) can be used to increase the faithfulness and coherence of assistants in challenging form-driven and content-driven prompts: in a human evaluation we show a 75\% preference for GPT4All using CFG over baseline.