Grokking Group Multiplication with Cosets
Paper and Code
Dec 11, 2023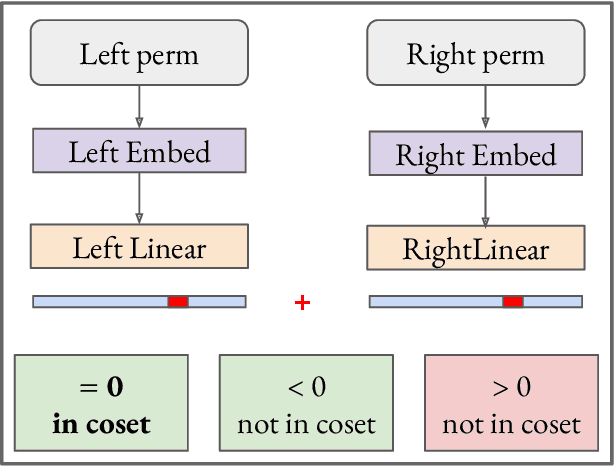
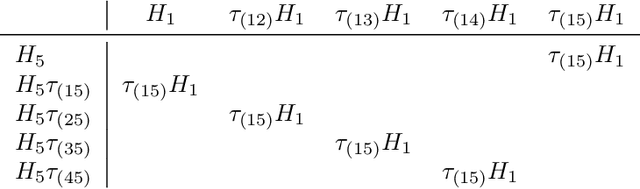
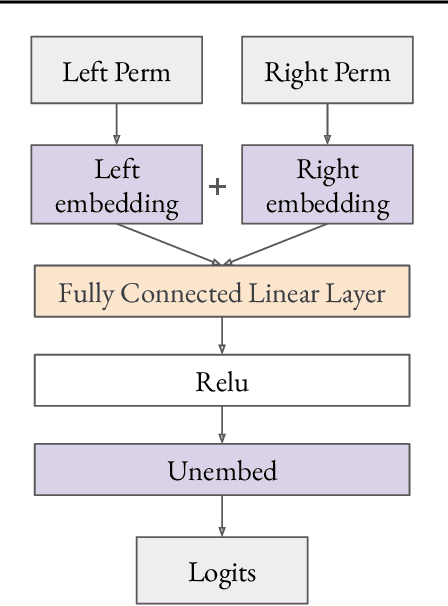
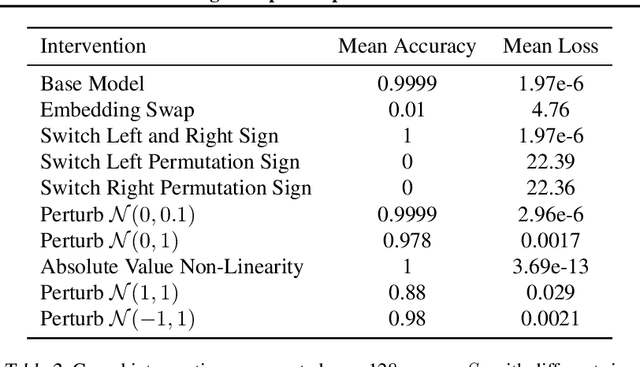
We use the group Fourier transform over the symmetric group $S_n$ to reverse engineer a 1-layer feedforward network that has "grokked" the multiplication of $S_5$ and $S_6$. Each model discovers the true subgroup structure of the full group and converges on circuits that decompose the group multiplication into the multiplication of the group's conjugate subgroups. We demonstrate the value of using the symmetries of the data and models to understand their mechanisms and hold up the ``coset circuit'' that the model uses as a fascinating example of the way neural networks implement computations. We also draw attention to current challenges in conducting mechanistic interpretability research by comparing our work to Chughtai et al. [6] which alleges to find a different algorithm for this same problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge