Extreme Event Prediction with Multi-agent Reinforcement Learning-based Parametrization of Atmospheric and Oceanic Turbulence

Global climate models (GCMs) are the main tools for understanding and predicting climate change. However, due to limited numerical resolutions, these models suffer from major structural uncertainties; e.g., they cannot resolve critical processes such as small-scale eddies in atmospheric and oceanic turbulence. Thus, such small-scale processes have to be represented as a function of the resolved scales via closures (parametrization). The accuracy of these closures is particularly important for capturing climate extremes. Traditionally, such closures are based on heuristics and simplifying assumptions about the unresolved physics. Recently, supervised-learned closures, trained offline on high-fidelity data, have been shown to outperform the classical physics-based closures. However, this approach requires a significant amount of high-fidelity training data and can also lead to instabilities. Reinforcement learning is emerging as a potent alternative for developing such closures as it requires only low-order statistics and leads to stable closures. In Scientific Multi-Agent Reinforcement Learning (SMARL) computational elements serve a dual role of discretization points and learning agents. We leverage SMARL and fundamentals of turbulence physics to learn closures for prototypes of atmospheric and oceanic turbulence. The policy is trained using only the enstrophy spectrum, which is nearly invariant and can be estimated from a few high-fidelity samples (these few samples are far from enough for supervised/offline learning). We show that these closures lead to stable low-resolution simulations that, at a fraction of the cost, can reproduce the high-fidelity simulations' statistics, including the tails of the probability density functions. The results demonstrate the high potential of SMARL for closure modeling for GCMs, especially in the regime of scarce data and indirect observations.

Learning Closed-form Equations for Subgrid-scale Closures from High-fidelity Data: Promises and Challenges

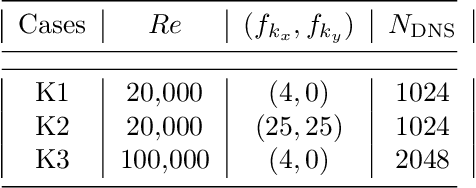
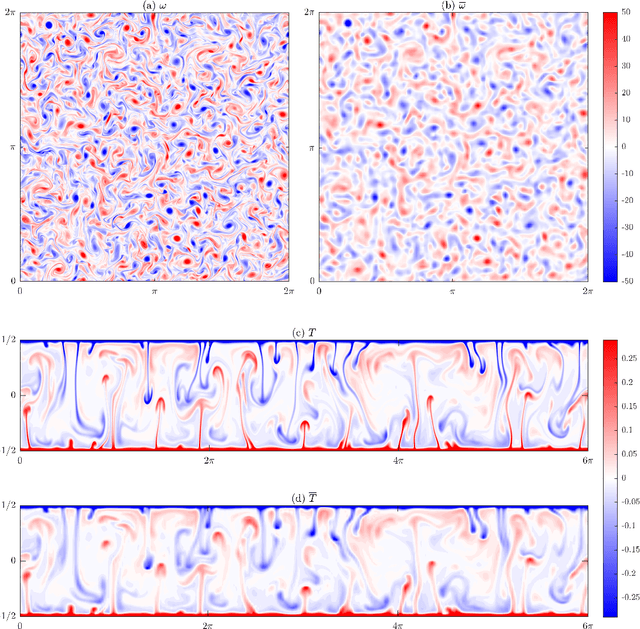
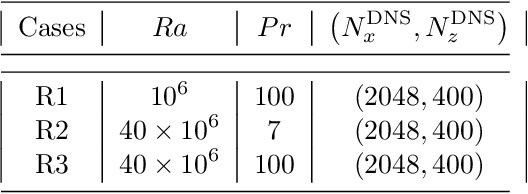
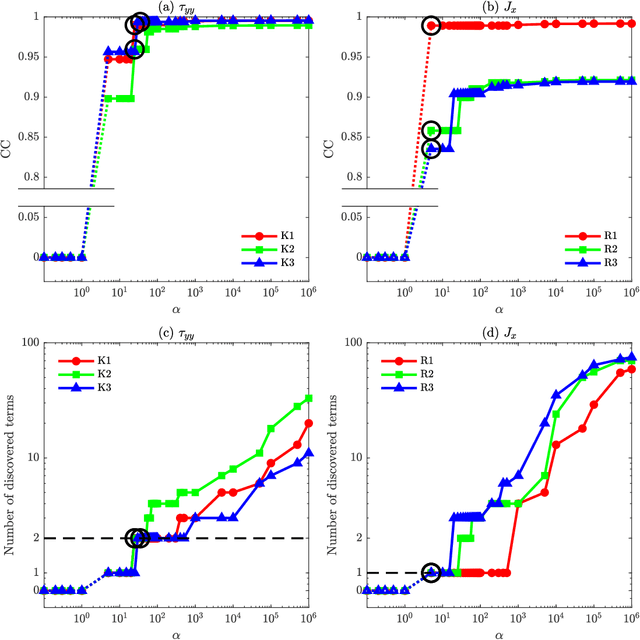
There is growing interest in discovering interpretable, closed-form equations for subgrid-scale (SGS) closures/parameterizations of complex processes in Earth system. Here, we apply a common equation-discovery technique with expansive libraries to learn closures from filtered direct numerical simulations of 2D forced turbulence and Rayleigh-B\'enard convection (RBC). Across common filters, we robustly discover closures of the same form for momentum and heat fluxes. These closures depend on nonlinear combinations of gradients of filtered variables (velocity, temperature), with constants that are independent of the fluid/flow properties and only depend on filter type/size. We show that these closures are the nonlinear gradient model (NGM), which is derivable analytically using Taylor-series expansions. In fact, we suggest that with common (physics-free) equation-discovery algorithms, regardless of the system/physics, discovered closures are always consistent with the Taylor-series. Like previous studies, we find that large-eddy simulations with NGM closures are unstable, despite significant similarities between the true and NGM-predicted fluxes (pattern correlations $> 0.95$). We identify two shortcomings as reasons for these instabilities: in 2D, NGM produces zero kinetic energy transfer between resolved and subgrid scales, lacking both diffusion and backscattering. In RBC, backscattering of potential energy is poorly predicted. Moreover, we show that SGS fluxes diagnosed from data, presumed the "truth" for discovery, depend on filtering procedures and are not unique. Accordingly, to learn accurate, stable closures from high-fidelity data in future work, we propose several ideas around using physics-informed libraries, loss functions, and metrics. These findings are relevant beyond turbulence to closure modeling of any multi-scale system.

Lagrangian PINNs: A causality-conforming solution to failure modes of physics-informed neural networks

Physics-informed neural networks (PINNs) leverage neural-networks to find the solutions of partial differential equation (PDE)-constrained optimization problems with initial conditions and boundary conditions as soft constraints. These soft constraints are often considered to be the sources of the complexity in the training phase of PINNs. Here, we demonstrate that the challenge of training (i) persists even when the boundary conditions are strictly enforced, and (ii) is closely related to the Kolmogorov n-width associated with problems demonstrating transport, convection, traveling waves, or moving fronts. Given this realization, we describe the mechanism underlying the training schemes such as those used in eXtended PINNs (XPINN), curriculum regularization, and sequence-to-sequence learning. For an important category of PDEs, i.e., governed by non-linear convection-diffusion equation, we propose reformulating PINNs on a Lagrangian frame of reference, i.e., LPINNs, as a PDE-informed solution. A parallel architecture with two branches is proposed. One branch solves for the state variables on the characteristics, and the second branch solves for the low-dimensional characteristics curves. The proposed architecture conforms to the causality innate to the convection, and leverages the direction of travel of the information in the domain. Finally, we demonstrate that the loss landscapes of LPINNs are less sensitive to the so-called "complexity" of the problems, compared to those in the traditional PINNs in the Eulerian framework.

Closed-form discovery of structural errors in models of chaotic systems by integrating Bayesian sparse regression and data assimilation

Models used for many important engineering and natural systems are imperfect. The discrepancy between the mathematical representations of a true physical system and its imperfect model is called the model error. These model errors can lead to substantial difference between the numerical solutions of the model and the observations of the system, particularly in those involving nonlinear, multi-scale phenomena. Thus, there is substantial interest in reducing model errors, particularly through understanding their physics and sources and leveraging the rapid growth of observational data. Here we introduce a framework named MEDIDA: Model Error Discovery with Interpretability and Data Assimilation. MEDIDA only requires a working numerical solver of the model and a small number of noise-free or noisy sporadic observations of the system. In MEDIDA, first the model error is estimated from differences between the observed states and model-predicted states (the latter are obtained from a number of one-time-step numerical integrations from the previous observed states). If observations are noisy, a data assimilation (DA) technique such as ensemble Kalman filter (EnKF) is first used to provide a noise-free analysis state of the system, which is then used in estimating the model error. Finally, an equation-discovery technique, such as the relevance vector machine (RVM), a sparsity-promoting Bayesian method, is used to identify an interpretable, parsimonious, closed-form representation of the model error. Using the chaotic Kuramoto-Sivashinsky (KS) system as the test case, we demonstrate the excellent performance of MEDIDA in discovering different types of structural/parametric model errors, representing different types of missing physics, using noise-free and noisy observations.

Physics-aware registration based auto-encoder for convection dominated PDEs

We design a physics-aware auto-encoder to specifically reduce the dimensionality of solutions arising from convection-dominated nonlinear physical systems. Although existing nonlinear manifold learning methods seem to be compelling tools to reduce the dimensionality of data characterized by a large Kolmogorov n-width, they typically lack a straightforward mapping from the latent space to the high-dimensional physical space. Moreover, the realized latent variables are often hard to interpret. Therefore, many of these methods are often dismissed in the reduced order modeling of dynamical systems governed by the partial differential equations (PDEs). Accordingly, we propose an auto-encoder type nonlinear dimensionality reduction algorithm. The unsupervised learning problem trains a diffeomorphic spatio-temporal grid, that registers the output sequence of the PDEs on a non-uniform parameter/time-varying grid, such that the Kolmogorov n-width of the mapped data on the learned grid is minimized. We demonstrate the efficacy and interpretability of our approach to separate convection/advection from diffusion/scaling on various manufactured and physical systems.