Efficient Transonic Aeroelastic Model Reduction Using Optimized Sparse Multi-Input Polynomial Functionals

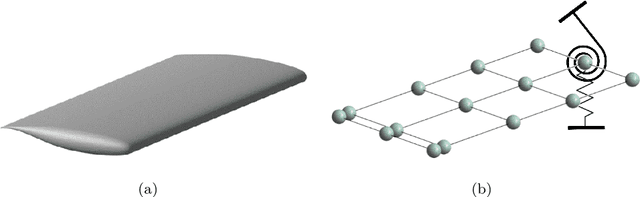
Nonlinear aeroelastic reduced-order models (ROMs) based on machine learning or artificial intelligence algorithms can be complex and computationally demanding to train, meaning that for practical aeroelastic applications, the conservative nature of linearization is often favored. Therefore, there is a requirement for novel nonlinear aeroelastic model reduction approaches that are accurate, simple and, most importantly, efficient to generate. This paper proposes a novel formulation for the identification of a compact multi-input Volterra series, where Orthogonal Matching Pursuit is used to obtain a set of optimally sparse nonlinear multi-input ROM coefficients from unsteady aerodynamic training data. The framework is exemplified using the Benchmark Supercritical Wing, considering; forced response, flutter and limit cycle oscillation. The simple and efficient Optimal Sparsity Multi-Input ROM (OSM-ROM) framework performs with high accuracy compared to the full-order aeroelastic model, requiring only a fraction of the tens-of-thousands of possible multi-input terms to be identified and allowing a 96% reduction in the number of training samples.

Lagrangian PINNs: A causality-conforming solution to failure modes of physics-informed neural networks

Physics-informed neural networks (PINNs) leverage neural-networks to find the solutions of partial differential equation (PDE)-constrained optimization problems with initial conditions and boundary conditions as soft constraints. These soft constraints are often considered to be the sources of the complexity in the training phase of PINNs. Here, we demonstrate that the challenge of training (i) persists even when the boundary conditions are strictly enforced, and (ii) is closely related to the Kolmogorov n-width associated with problems demonstrating transport, convection, traveling waves, or moving fronts. Given this realization, we describe the mechanism underlying the training schemes such as those used in eXtended PINNs (XPINN), curriculum regularization, and sequence-to-sequence learning. For an important category of PDEs, i.e., governed by non-linear convection-diffusion equation, we propose reformulating PINNs on a Lagrangian frame of reference, i.e., LPINNs, as a PDE-informed solution. A parallel architecture with two branches is proposed. One branch solves for the state variables on the characteristics, and the second branch solves for the low-dimensional characteristics curves. The proposed architecture conforms to the causality innate to the convection, and leverages the direction of travel of the information in the domain. Finally, we demonstrate that the loss landscapes of LPINNs are less sensitive to the so-called "complexity" of the problems, compared to those in the traditional PINNs in the Eulerian framework.

Physics-aware registration based auto-encoder for convection dominated PDEs

We design a physics-aware auto-encoder to specifically reduce the dimensionality of solutions arising from convection-dominated nonlinear physical systems. Although existing nonlinear manifold learning methods seem to be compelling tools to reduce the dimensionality of data characterized by a large Kolmogorov n-width, they typically lack a straightforward mapping from the latent space to the high-dimensional physical space. Moreover, the realized latent variables are often hard to interpret. Therefore, many of these methods are often dismissed in the reduced order modeling of dynamical systems governed by the partial differential equations (PDEs). Accordingly, we propose an auto-encoder type nonlinear dimensionality reduction algorithm. The unsupervised learning problem trains a diffeomorphic spatio-temporal grid, that registers the output sequence of the PDEs on a non-uniform parameter/time-varying grid, such that the Kolmogorov n-width of the mapped data on the learned grid is minimized. We demonstrate the efficacy and interpretability of our approach to separate convection/advection from diffusion/scaling on various manufactured and physical systems.

Deep convolutional recurrent autoencoders for learning low-dimensional feature dynamics of fluid systems

Model reduction of high-dimensional dynamical systems alleviates computational burdens faced in various tasks from design optimization to model predictive control. One popular model reduction approach is based on projecting the governing equations onto a subspace spanned by basis functions obtained from the compression of a dataset of solution snapshots. However, this method is intrusive since the projection requires access to the system operators. Further, some systems may require special treatment of nonlinearities to ensure computational efficiency or additional modeling to preserve stability. In this work we propose a deep learning-based strategy for nonlinear model reduction that is inspired by projection-based model reduction where the idea is to identify some optimal low-dimensional representation and evolve it in time. Our approach constructs a modular model consisting of a deep convolutional autoencoder and a modified LSTM network. The deep convolutional autoencoder returns a low-dimensional representation in terms of coordinates on some expressive nonlinear data-supporting manifold. The dynamics on this manifold are then modeled by the modified LSTM network in a computationally efficient manner. An offline unsupervised training strategy that exploits the model modularity is also developed. We demonstrate our model on three illustrative examples each highlighting the model's performance in prediction tasks for fluid systems with large parameter-variations and its stability in long-term prediction.