Machine learning in and out of equilibrium

The algorithms used to train neural networks, like stochastic gradient descent (SGD), have close parallels to natural processes that navigate a high-dimensional parameter space -- for example protein folding or evolution. Our study uses a Fokker-Planck approach, adapted from statistical physics, to explore these parallels in a single, unified framework. We focus in particular on the stationary state of the system in the long-time limit, which in conventional SGD is out of equilibrium, exhibiting persistent currents in the space of network parameters. As in its physical analogues, the current is associated with an entropy production rate for any given training trajectory. The stationary distribution of these rates obeys the integral and detailed fluctuation theorems -- nonequilibrium generalizations of the second law of thermodynamics. We validate these relations in two numerical examples, a nonlinear regression network and MNIST digit classification. While the fluctuation theorems are universal, there are other aspects of the stationary state that are highly sensitive to the training details. Surprisingly, the effective loss landscape and diffusion matrix that determine the shape of the stationary distribution vary depending on the simple choice of minibatching done with or without replacement. We can take advantage of this nonequilibrium sensitivity to engineer an equilibrium stationary state for a particular application: sampling from a posterior distribution of network weights in Bayesian machine learning. We propose a new variation of stochastic gradient Langevin dynamics (SGLD) that harnesses without replacement minibatching. In an example system where the posterior is exactly known, this SGWORLD algorithm outperforms SGLD, converging to the posterior orders of magnitude faster as a function of the learning rate.

Principal Trade-off Analysis

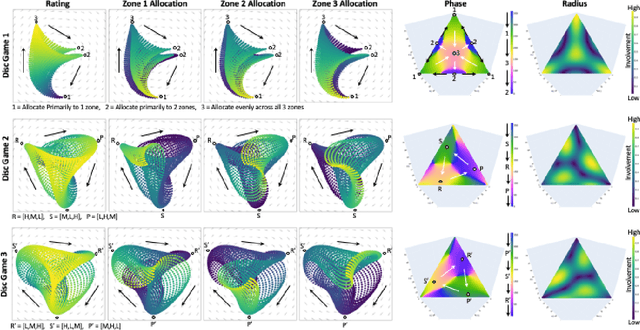
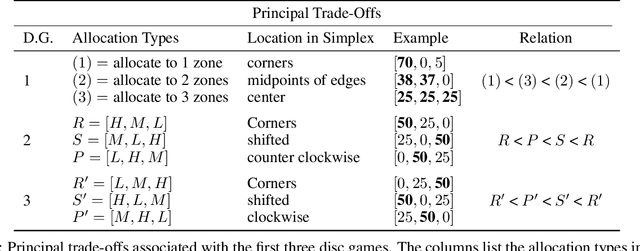
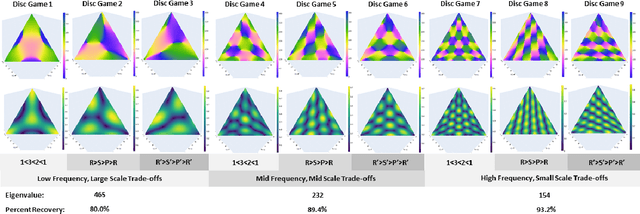
This paper develops Principal Trade-off Analysis (PTA), a decomposition method, analogous to Principal Component Analysis (PCA), which permits the representation of any game as the weighted sum of disc games (continuous R-P-S games). Applying PTA to empirically generated tournament graphs produces a sequence of embeddings into orthogonal 2D feature planes representing independent strategic trade-offs. Each trade-off generates a mode of cyclic competition. Like PCA, PTA provides optimal low rank estimates of the tournament graphs that can be truncated for approximation. The complexity of cyclic competition can be quantified by computing the number of significant cyclic modes. We illustrate the PTA via application to a pair of games (Blotto, Pokemon). The resulting 2D disc game representations are shown to be well suited for visualization and are easily interpretable. In Blotto, PTA identifies game symmetries, and specifies strategic trade-offs associated with distinct win conditions. For Pokemon, PTA embeddings produce clusters in the embedding space that naturally correspond to Pokemon types, a design in the game that produces cyclic trade offs.

A Variational Inference Approach to Inverse Problems with Gamma Hyperpriors

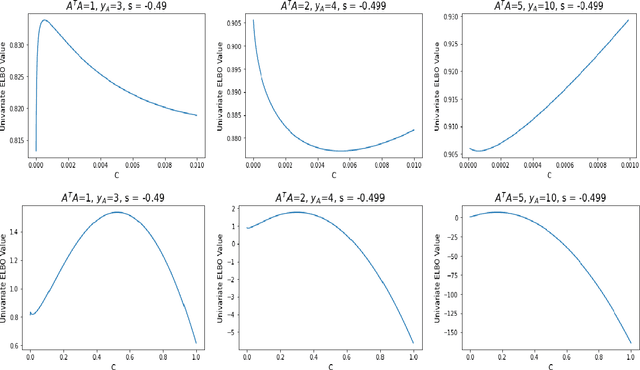
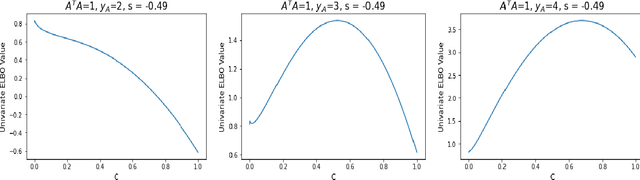
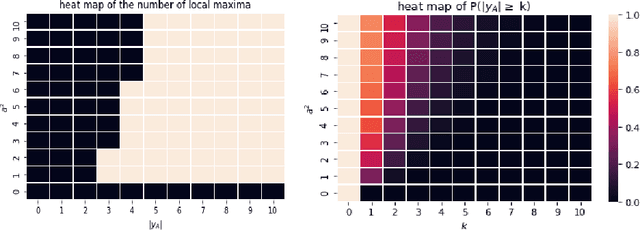
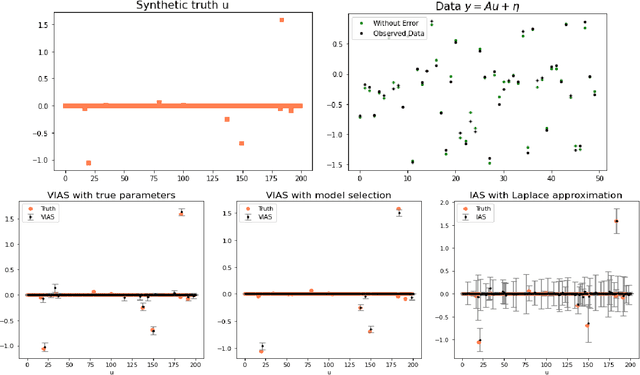
Hierarchical models with gamma hyperpriors provide a flexible, sparse-promoting framework to bridge $L^1$ and $L^2$ regularizations in Bayesian formulations to inverse problems. Despite the Bayesian motivation for these models, existing methodologies are limited to \textit{maximum a posteriori} estimation. The potential to perform uncertainty quantification has not yet been realized. This paper introduces a variational iterative alternating scheme for hierarchical inverse problems with gamma hyperpriors. The proposed variational inference approach yields accurate reconstruction, provides meaningful uncertainty quantification, and is easy to implement. In addition, it lends itself naturally to conduct model selection for the choice of hyperparameters. We illustrate the performance of our methodology in several computed examples, including a deconvolution problem and sparse identification of dynamical systems from time series data.