Bayesian Optimization with Noise-Free Observations: Improved Regret Bounds via Random Exploration
Paper and Code
Jan 30, 2024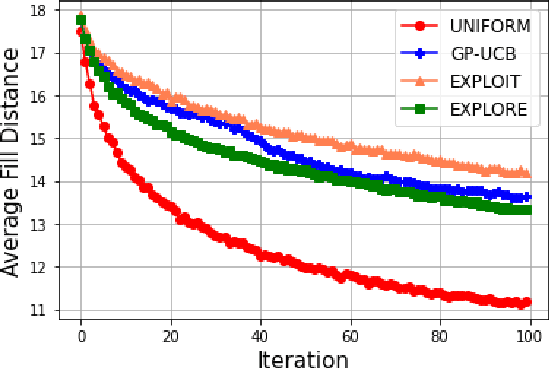
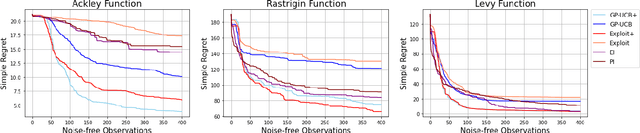
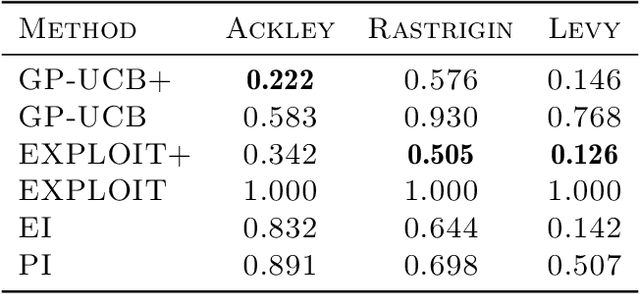
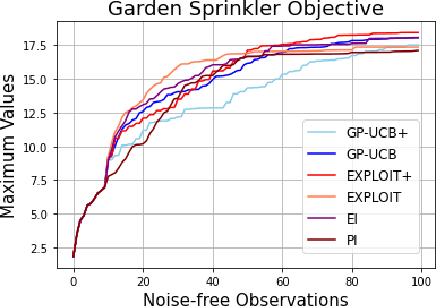
This paper studies Bayesian optimization with noise-free observations. We introduce new algorithms rooted in scattered data approximation that rely on a random exploration step to ensure that the fill-distance of query points decays at a near-optimal rate. Our algorithms retain the ease of implementation of the classical GP-UCB algorithm and satisfy cumulative regret bounds that nearly match those conjectured in arXiv:2002.05096, hence solving a COLT open problem. Furthermore, the new algorithms outperform GP-UCB and other popular Bayesian optimization strategies in several examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge