Probabilistic operator learning: generative modeling and uncertainty quantification for foundation models of differential equations

In-context operator networks (ICON) are a class of operator learning methods based on the novel architectures of foundation models. Trained on a diverse set of datasets of initial and boundary conditions paired with corresponding solutions to ordinary and partial differential equations (ODEs and PDEs), ICON learns to map example condition-solution pairs of a given differential equation to an approximation of its solution operator. Here, we present a probabilistic framework that reveals ICON as implicitly performing Bayesian inference, where it computes the mean of the posterior predictive distribution over solution operators conditioned on the provided context, i.e., example condition-solution pairs. The formalism of random differential equations provides the probabilistic framework for describing the tasks ICON accomplishes while also providing a basis for understanding other multi-operator learning methods. This probabilistic perspective provides a basis for extending ICON to \emph{generative} settings, where one can sample from the posterior predictive distribution of solution operators. The generative formulation of ICON (GenICON) captures the underlying uncertainty in the solution operator, which enables principled uncertainty quantification in the solution predictions in operator learning.

Proximal optimal transport divergences

We introduce proximal optimal transport divergence, a novel discrepancy measure that interpolates between information divergences and optimal transport distances via an infimal convolution formulation. This divergence provides a principled foundation for optimal transport proximals and proximal optimization methods frequently used in generative modeling. We explore its mathematical properties, including smoothness, boundedness, and computational tractability, and establish connections to primal-dual formulation and adversarial learning. Building on the Benamou-Brenier dynamic formulation of optimal transport cost, we also establish a dynamic formulation for proximal OT divergences. The resulting dynamic formulation is a first order mean-field game whose optimality conditions are governed by a pair of nonlinear partial differential equations, a backward Hamilton-Jacobi and a forward continuity partial differential equations. Our framework generalizes existing approaches while offering new insights and computational tools for generative modeling, distributional optimization, and gradient-based learning in probability spaces.

Equivariant score-based generative models provably learn distributions with symmetries efficiently

Symmetry is ubiquitous in many real-world phenomena and tasks, such as physics, images, and molecular simulations. Empirical studies have demonstrated that incorporating symmetries into generative models can provide better generalization and sampling efficiency when the underlying data distribution has group symmetry. In this work, we provide the first theoretical analysis and guarantees of score-based generative models (SGMs) for learning distributions that are invariant with respect to some group symmetry and offer the first quantitative comparison between data augmentation and adding equivariant inductive bias. First, building on recent works on the Wasserstein-1 ($\mathbf{d}_1$) guarantees of SGMs and empirical estimations of probability divergences under group symmetry, we provide an improved $\mathbf{d}_1$ generalization bound when the data distribution is group-invariant. Second, we describe the inductive bias of equivariant SGMs using Hamilton-Jacobi-Bellman theory, and rigorously demonstrate that one can learn the score of a symmetrized distribution using equivariant vector fields without data augmentations through the analysis of the optimality and equivalence of score-matching objectives. This also provides practical guidance that one does not have to augment the dataset as long as the vector field or the neural network parametrization is equivariant. Moreover, we quantify the impact of not incorporating equivariant structure into the score parametrization, by showing that non-equivariant vector fields can yield worse generalization bounds. This can be viewed as a type of model-form error that describes the missing structure of non-equivariant vector fields. Numerical simulations corroborate our analysis and highlight that data augmentations cannot replace the role of equivariant vector fields.

Combining Wasserstein-1 and Wasserstein-2 proximals: robust manifold learning via well-posed generative flows

We formulate well-posed continuous-time generative flows for learning distributions that are supported on low-dimensional manifolds through Wasserstein proximal regularizations of $f$-divergences. Wasserstein-1 proximal operators regularize $f$-divergences so that singular distributions can be compared. Meanwhile, Wasserstein-2 proximal operators regularize the paths of the generative flows by adding an optimal transport cost, i.e., a kinetic energy penalization. Via mean-field game theory, we show that the combination of the two proximals is critical for formulating well-posed generative flows. Generative flows can be analyzed through optimality conditions of a mean-field game (MFG), a system of a backward Hamilton-Jacobi (HJ) and a forward continuity partial differential equations (PDEs) whose solution characterizes the optimal generative flow. For learning distributions that are supported on low-dimensional manifolds, the MFG theory shows that the Wasserstein-1 proximal, which addresses the HJ terminal condition, and the Wasserstein-2 proximal, which addresses the HJ dynamics, are both necessary for the corresponding backward-forward PDE system to be well-defined and have a unique solution with provably linear flow trajectories. This implies that the corresponding generative flow is also unique and can therefore be learned in a robust manner even for learning high-dimensional distributions supported on low-dimensional manifolds. The generative flows are learned through adversarial training of continuous-time flows, which bypasses the need for reverse simulation. We demonstrate the efficacy of our approach for generating high-dimensional images without the need to resort to autoencoders or specialized architectures.

Score-based generative models are provably robust: an uncertainty quantification perspective

Through an uncertainty quantification (UQ) perspective, we show that score-based generative models (SGMs) are provably robust to the multiple sources of error in practical implementation. Our primary tool is the Wasserstein uncertainty propagation (WUP) theorem, a model-form UQ bound that describes how the $L^2$ error from learning the score function propagates to a Wasserstein-1 ($\mathbf{d}_1$) ball around the true data distribution under the evolution of the Fokker-Planck equation. We show how errors due to (a) finite sample approximation, (b) early stopping, (c) score-matching objective choice, (d) score function parametrization expressiveness, and (e) reference distribution choice, impact the quality of the generative model in terms of a $\mathbf{d}_1$ bound of computable quantities. The WUP theorem relies on Bernstein estimates for Hamilton-Jacobi-Bellman partial differential equations (PDE) and the regularizing properties of diffusion processes. Specifically, PDE regularity theory shows that stochasticity is the key mechanism ensuring SGM algorithms are provably robust. The WUP theorem applies to integral probability metrics beyond $\mathbf{d}_1$, such as the total variation distance and the maximum mean discrepancy. Sample complexity and generalization bounds in $\mathbf{d}_1$ follow directly from the WUP theorem. Our approach requires minimal assumptions, is agnostic to the manifold hypothesis and avoids absolute continuity assumptions for the target distribution. Additionally, our results clarify the trade-offs among multiple error sources in SGMs.

Wasserstein proximal operators describe score-based generative models and resolve memorization

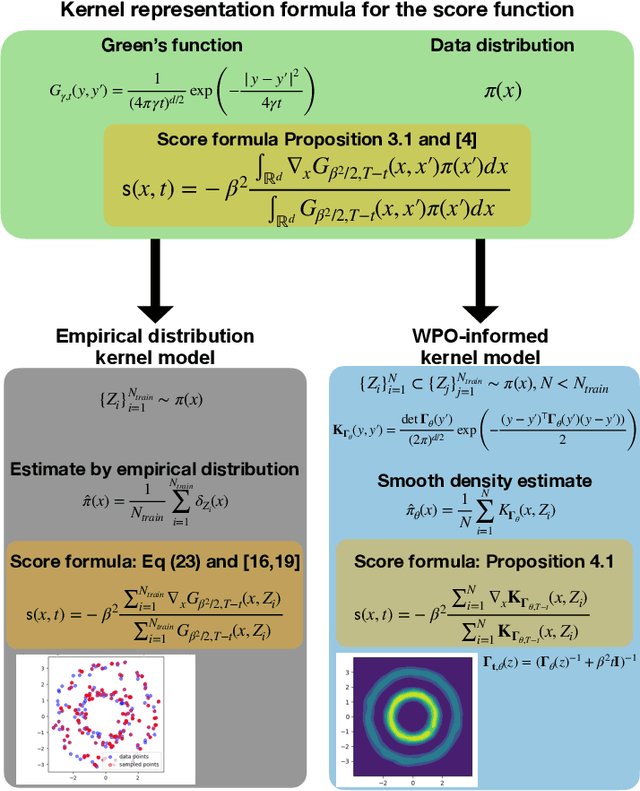
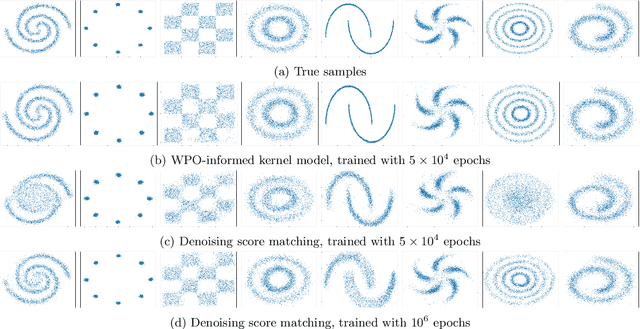
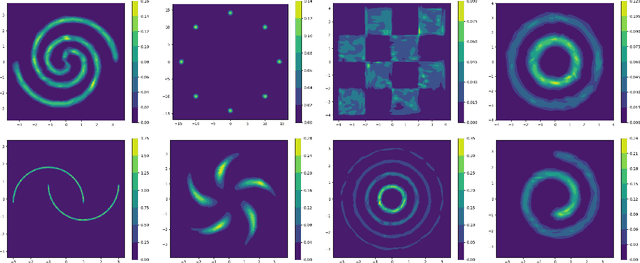
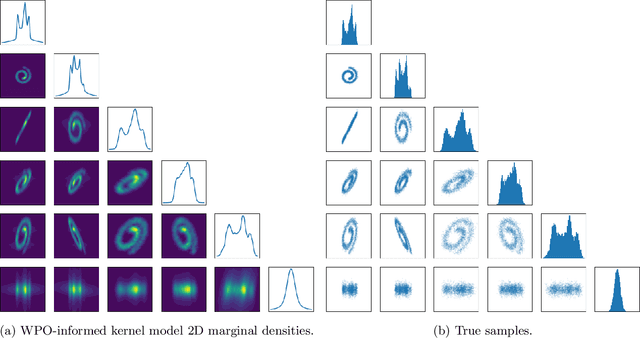
We focus on the fundamental mathematical structure of score-based generative models (SGMs). We first formulate SGMs in terms of the Wasserstein proximal operator (WPO) and demonstrate that, via mean-field games (MFGs), the WPO formulation reveals mathematical structure that describes the inductive bias of diffusion and score-based models. In particular, MFGs yield optimality conditions in the form of a pair of coupled partial differential equations: a forward-controlled Fokker-Planck (FP) equation, and a backward Hamilton-Jacobi-Bellman (HJB) equation. Via a Cole-Hopf transformation and taking advantage of the fact that the cross-entropy can be related to a linear functional of the density, we show that the HJB equation is an uncontrolled FP equation. Second, with the mathematical structure at hand, we present an interpretable kernel-based model for the score function which dramatically improves the performance of SGMs in terms of training samples and training time. In addition, the WPO-informed kernel model is explicitly constructed to avoid the recently studied memorization effects of score-based generative models. The mathematical form of the new kernel-based models in combination with the use of the terminal condition of the MFG reveals new explanations for the manifold learning and generalization properties of SGMs, and provides a resolution to their memorization effects. Finally, our mathematically informed, interpretable kernel-based model suggests new scalable bespoke neural network architectures for high-dimensional applications.

A mean-field games laboratory for generative modeling

In this paper, we demonstrate the versatility of mean-field games (MFGs) as a mathematical framework for explaining, enhancing, and designing generative models. There is a pervasive sense in the generative modeling community that the various flow and diffusion-based generative models have some common foundational structure and interrelationships. We establish connections between MFGs and major classes of flow and diffusion-based generative models including continuous-time normalizing flows, score-based models, and Wasserstein gradient flows. We derive these three classes of generative models through different choices of particle dynamics and cost functions. Furthermore, we study the mathematical structure and properties of each generative model by studying their associated MFG's optimality condition, which is a set of coupled forward-backward nonlinear partial differential equations (PDEs). The theory of MFGs, therefore, enables the study of generative models through the theory of nonlinear PDEs. Through this perspective, we investigate the well-posedness and structure of normalizing flows, unravel the mathematical structure of score-based generative modeling, and derive a mean-field game formulation of the Wasserstein gradient flow. From an algorithmic perspective, the optimality conditions of MFGs also allow us to introduce HJB regularizers for enhanced training of a broad class of generative models. In particular, we propose and demonstrate an Hamilton-Jacobi-Bellman regularized SGM with improved performance over standard SGMs. We present this framework as an MFG laboratory which serves as a platform for revealing new avenues of experimentation and invention of generative models. This laboratory will give rise to a multitude of well-posed generative modeling formulations and will provide a consistent theoretical framework upon which numerical and algorithmic tools may be developed.

Transport map unadjusted Langevin algorithms

Langevin dynamics are widely used in sampling high-dimensional, non-Gaussian distributions whose densities are known up to a normalizing constant. In particular, there is strong interest in unadjusted Langevin algorithms (ULA), which directly discretize Langevin dynamics to estimate expectations over the target distribution. We study the use of transport maps that approximately normalize a target distribution as a way to precondition and accelerate the convergence of Langevin dynamics. We show that in continuous time, when a transport map is applied to Langevin dynamics, the result is a Riemannian manifold Langevin dynamics (RMLD) with metric defined by the transport map. This connection suggests more systematic ways of learning metrics, and also yields alternative discretizations of the RMLD described by the map, which we study. Moreover, we show that under certain conditions, when the transport map is used in conjunction with ULA, we can improve the geometric rate of convergence of the output process in the 2--Wasserstein distance. Illustrative numerical results complement our theoretical claims.

Geometry-informed irreversible perturbations for accelerated convergence of Langevin dynamics

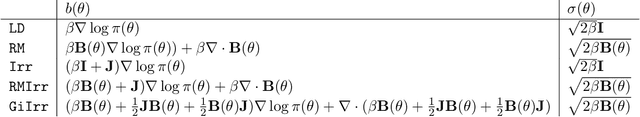
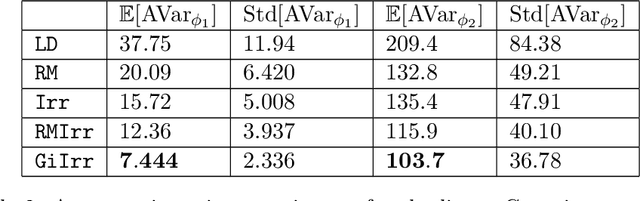
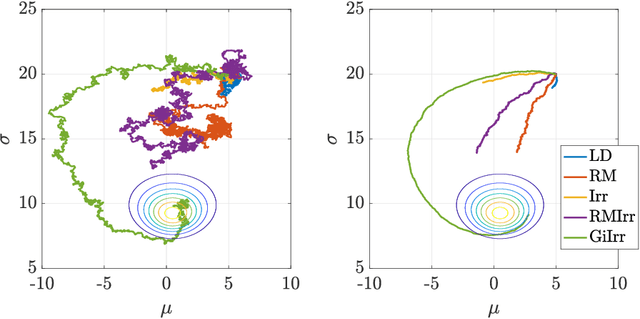
We introduce a novel geometry-informed irreversible perturbation that accelerates convergence of the Langevin algorithm for Bayesian computation. It is well documented that there exist perturbations to the Langevin dynamics that preserve its invariant measure while accelerating its convergence. Irreversible perturbations and reversible perturbations (such as Riemannian manifold Langevin dynamics (RMLD)) have separately been shown to improve the performance of Langevin samplers. We consider these two perturbations simultaneously by presenting a novel form of irreversible perturbation for RMLD that is informed by the underlying geometry. Through numerical examples, we show that this new irreversible perturbation can improve performance of the estimator over reversible perturbations that do not take the geometry into account. Moreover we demonstrate that irreversible perturbations generally can be implemented in conjunction with the stochastic gradient version of the Langevin algorithm. Lastly, while continuous-time irreversible perturbations cannot impair the performance of a Langevin estimator, the situation can sometimes be more complicated when discretization is considered. To this end, we describe a discrete-time example in which irreversibility increases both the bias and variance of the resulting estimator.