Wasserstein proximal operators describe score-based generative models and resolve memorization

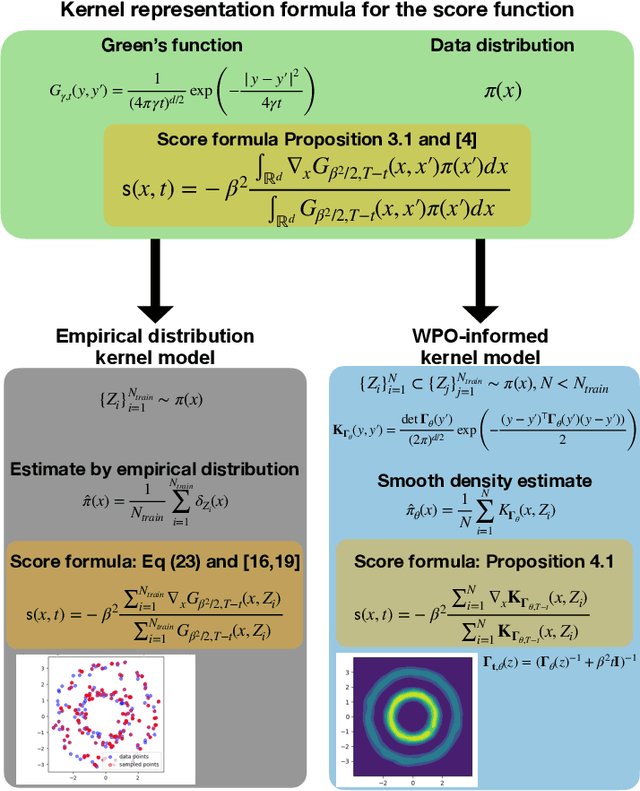
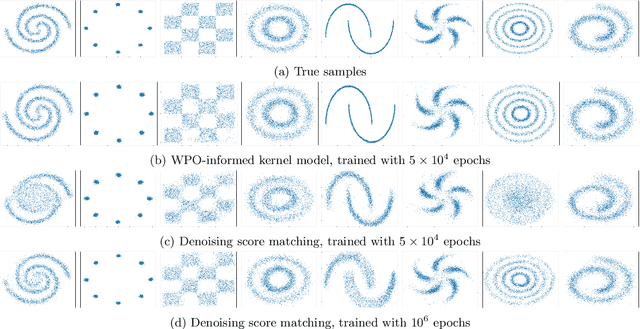
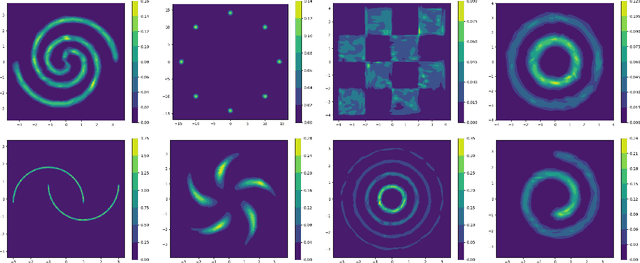
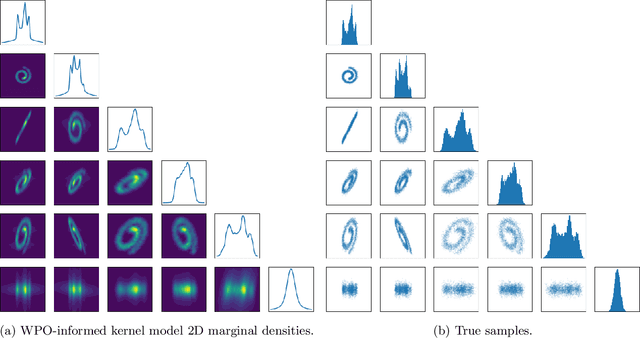
We focus on the fundamental mathematical structure of score-based generative models (SGMs). We first formulate SGMs in terms of the Wasserstein proximal operator (WPO) and demonstrate that, via mean-field games (MFGs), the WPO formulation reveals mathematical structure that describes the inductive bias of diffusion and score-based models. In particular, MFGs yield optimality conditions in the form of a pair of coupled partial differential equations: a forward-controlled Fokker-Planck (FP) equation, and a backward Hamilton-Jacobi-Bellman (HJB) equation. Via a Cole-Hopf transformation and taking advantage of the fact that the cross-entropy can be related to a linear functional of the density, we show that the HJB equation is an uncontrolled FP equation. Second, with the mathematical structure at hand, we present an interpretable kernel-based model for the score function which dramatically improves the performance of SGMs in terms of training samples and training time. In addition, the WPO-informed kernel model is explicitly constructed to avoid the recently studied memorization effects of score-based generative models. The mathematical form of the new kernel-based models in combination with the use of the terminal condition of the MFG reveals new explanations for the manifold learning and generalization properties of SGMs, and provides a resolution to their memorization effects. Finally, our mathematically informed, interpretable kernel-based model suggests new scalable bespoke neural network architectures for high-dimensional applications.

Prompting In-Context Operator Learning with Sensor Data, Equations, and Natural Language

In the growing domain of scientific machine learning, in-context operator learning has demonstrated notable potential in learning operators from prompted data during inference stage without weight updates. However, the current model's overdependence on sensor data, may inadvertently overlook the invaluable human insight into the operator. To address this, we present a transformation of in-context operator learning into a multi-modal paradigm. We propose the use of "captions" to integrate human knowledge about the operator, expressed through natural language descriptions and equations. We illustrate how this method not only broadens the flexibility and generality of physics-informed learning, but also significantly boosts learning performance and reduces data needs. Furthermore, we introduce a more efficient neural network architecture for multi-modal in-context operator learning, referred to as "ICON-LM", based on a language-model-like architecture. We demonstrate the viability of "ICON-LM" for scientific machine learning tasks, which creates a new path for the application of language models.

In-Context Operator Learning for Differential Equation Problems

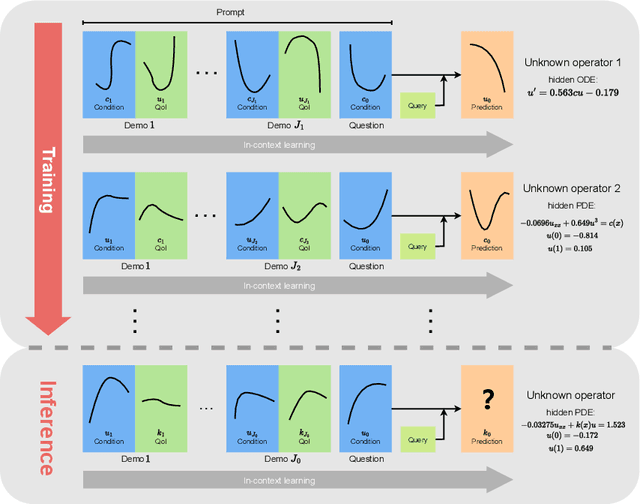
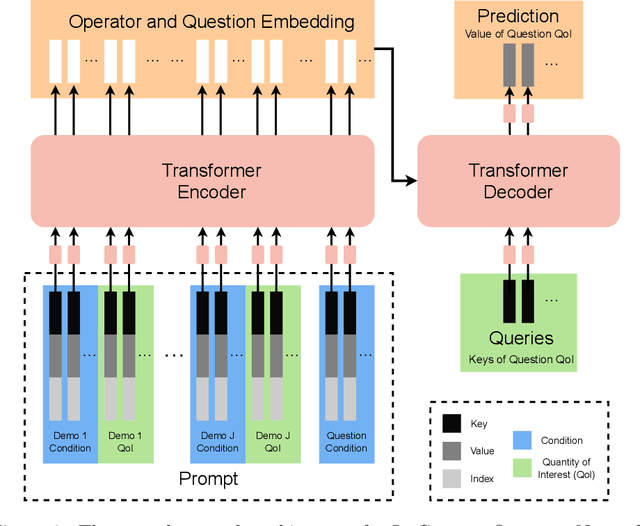
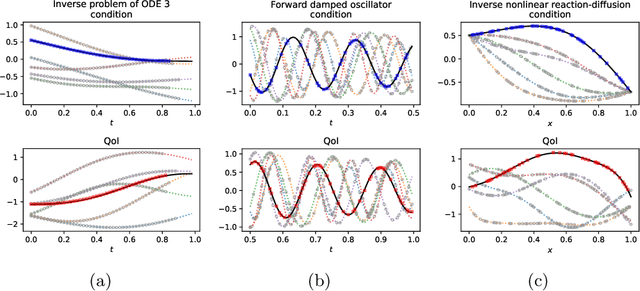
This paper introduces a new neural-network-based approach, namely IN-context Differential Equation Encoder-Decoder (INDEED), to simultaneously learn operators from data and apply it to new questions during the inference stage, without any weight update. Existing methods are limited to using a neural network to approximate a specific equation solution or a specific operator, requiring retraining when switching to a new problem with different equations. By training a single neural network as an operator learner, we can not only get rid of retraining (even fine-tuning) the neural network for new problems, but also leverage the commonalities shared across operators so that only a few demos are needed when learning a new operator. Our numerical results show the neural network's capability as a few-shot operator learner for a diversified type of differential equation problems, including forward and inverse problems of ODEs and PDEs, and also show that it can generalize its learning capability to operators beyond the training distribution, even to an unseen type of operator.

Fault-Tolerant Deep Learning: A Hierarchical Perspective

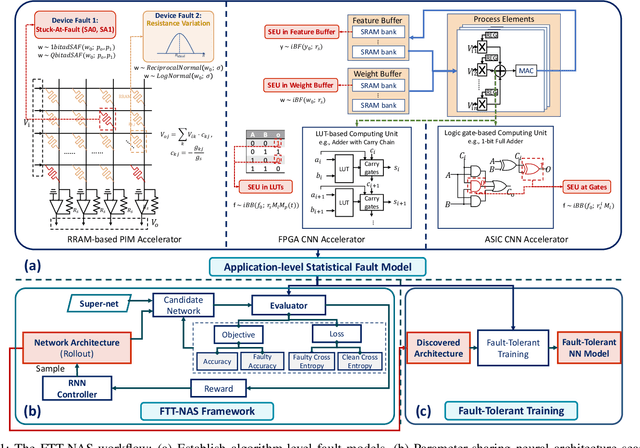
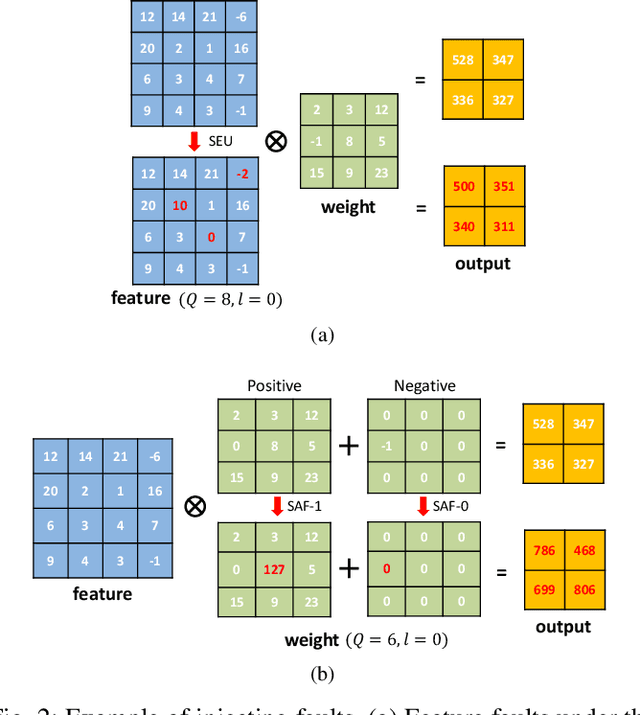
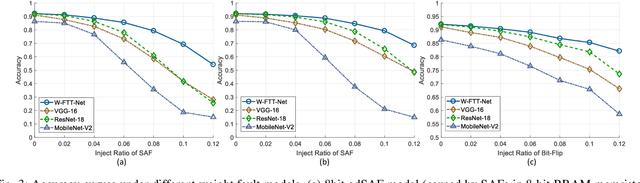
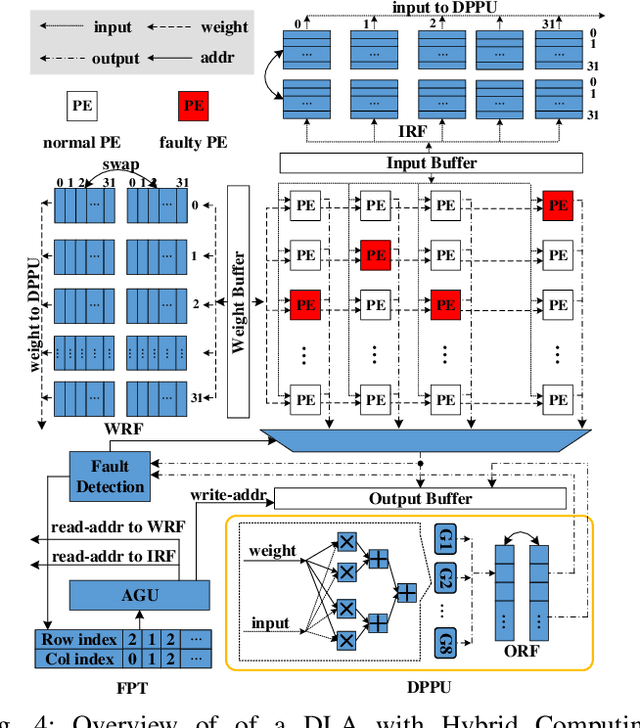
With the rapid advancements of deep learning in the past decade, it can be foreseen that deep learning will be continuously deployed in more and more safety-critical applications such as autonomous driving and robotics. In this context, reliability turns out to be critical to the deployment of deep learning in these applications and gradually becomes a first-class citizen among the major design metrics like performance and energy efficiency. Nevertheless, the back-box deep learning models combined with the diverse underlying hardware faults make resilient deep learning extremely challenging. In this special session, we conduct a comprehensive survey of fault-tolerant deep learning design approaches with a hierarchical perspective and investigate these approaches from model layer, architecture layer, circuit layer, and cross layer respectively.