Optimizing Decoding Paths in Masked Diffusion Models by Quantifying Uncertainty

Masked Diffusion Models (MDMs) offer flexible, non-autoregressive generation, but this freedom introduces a challenge: final output quality is highly sensitive to the decoding order. We are the first to formalize this issue, attributing the variability in output quality to the cumulative predictive uncertainty along a generative path. To quantify this uncertainty, we introduce Denoising Entropy, a computable metric that serves as an internal signal for evaluating generative process. Leveraging this metric, we propose two algorithms designed to optimize the decoding path: a post-hoc selection method and a real-time guidance strategy. Experiments demonstrate that our entropy-guided methods significantly improve generation quality, consistently boosting accuracy on challenging reasoning, planning, and code benchmarks. Our work establishes Denoising Entropy as a principled tool for understanding and controlling generation, effectively turning the uncertainty in MDMs from a liability into a key advantage for discovering high-quality solutions.

Towards Efficient and Effective Multi-Camera Encoding for End-to-End Driving

We present Flex, an efficient and effective scene encoder that addresses the computational bottleneck of processing high-volume multi-camera data in end-to-end autonomous driving. Flex employs a small set of learnable scene tokens to jointly encode information from all image tokens across different cameras and timesteps. By design, our approach is geometry-agnostic, learning a compact scene representation directly from data without relying on the explicit 3D inductive biases, such as Bird-Eye-View (BEV), occupancy or tri-plane representations, which are common in prior work. This holistic encoding strategy aggressively compresses the visual input for the downstream Large Language Model (LLM) based policy model. Evaluated on a large-scale proprietary dataset of 20,000 driving hours, our Flex achieves 2.2x greater inference throughput while improving driving performance by a large margin compared to state-of-the-art methods. Furthermore, we show that these compact scene tokens develop an emergent capability for scene decomposition without any explicit supervision. Our findings challenge the prevailing assumption that 3D priors are necessary, demonstrating that a data-driven, joint encoding strategy offers a more scalable, efficient and effective path for future autonomous driving systems.

A Survey on Reconfigurable Intelligent Surfaces in Practical Systems: Security and Privacy Perspectives

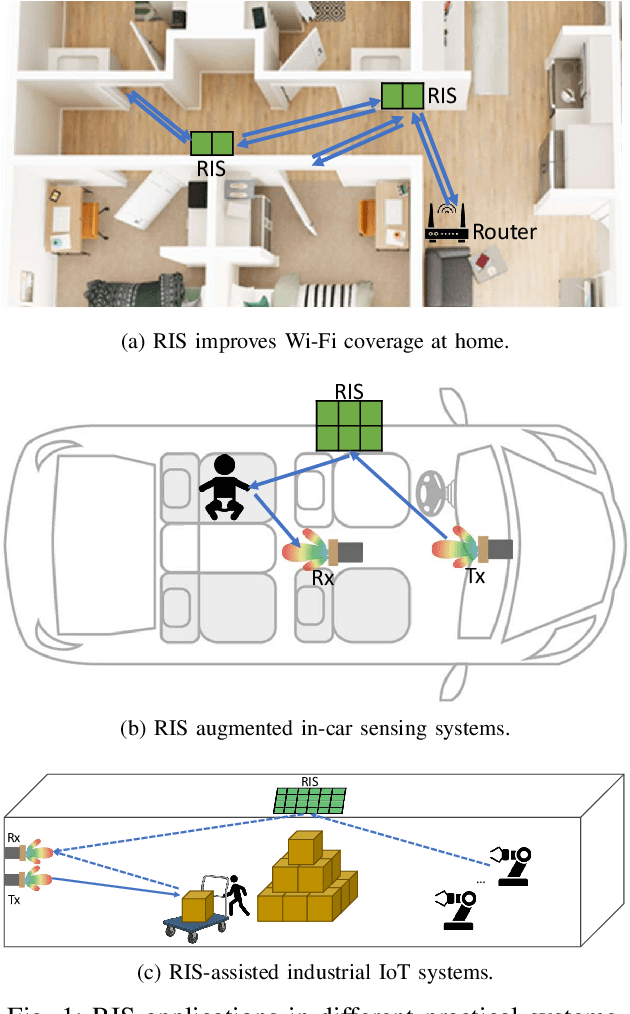
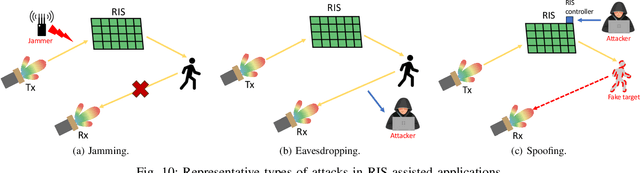
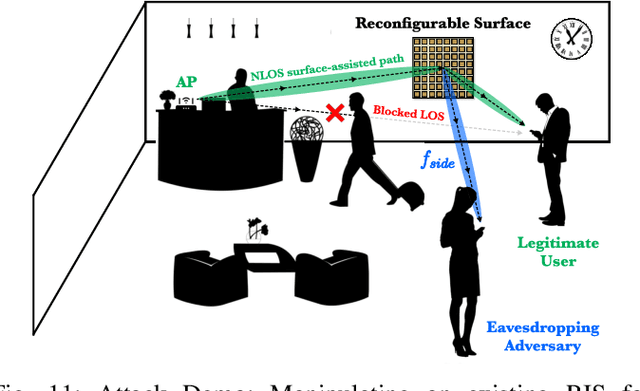
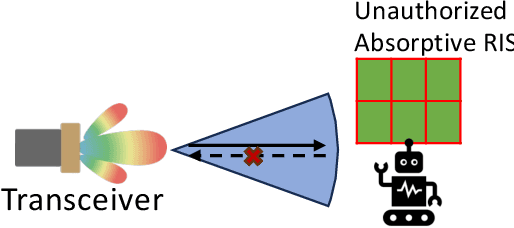
Reconfigurable Intelligent Surfaces (RIS) have emerged as a transformative technology capable of reshaping wireless environments through dynamic manipulation of electromagnetic waves. While extensive research has explored their theoretical benefits for communication and sensing, practical deployments in smart environments such as homes, vehicles, and industrial settings remain limited and under-examined, particularly from security and privacy perspectives. This survey provides a comprehensive examination of RIS applications in real-world systems, with a focus on the security and privacy threats, vulnerabilities, and defensive strategies relevant to practical use. We analyze scenarios with two types of systems (with and without legitimate RIS) and two types of attackers (with and without malicious RIS), and demonstrate how RIS may introduce new attacks to practical systems, including eavesdropping, jamming, and spoofing attacks. In response, we review defenses against RIS-related attacks in these systems, such as applying additional security algorithms, disrupting attackers, and early detection of unauthorized RIS. We also discuss scenarios in which the legitimate user applies an additional RIS to defend against attacks. To support future research, we also provide a collection of open-source tools, datasets, demos, and papers at: https://awesome-ris-security.github.io/. By highlighting RIS's functionality and its security/privacy challenges and opportunities, this survey aims to guide researchers and engineers toward the development of secure, resilient, and privacy-preserving RIS-enabled practical wireless systems and environments.

FASIONAD++ : Integrating High-Level Instruction and Information Bottleneck in FAt-Slow fusION Systems for Enhanced Safety in Autonomous Driving with Adaptive Feedback

Ensuring safe, comfortable, and efficient planning is crucial for autonomous driving systems. While end-to-end models trained on large datasets perform well in standard driving scenarios, they struggle with complex low-frequency events. Recent Large Language Models (LLMs) and Vision Language Models (VLMs) advancements offer enhanced reasoning but suffer from computational inefficiency. Inspired by the dual-process cognitive model "Thinking, Fast and Slow", we propose $\textbf{FASIONAD}$ -- a novel dual-system framework that synergizes a fast end-to-end planner with a VLM-based reasoning module. The fast system leverages end-to-end learning to achieve real-time trajectory generation in common scenarios, while the slow system activates through uncertainty estimation to perform contextual analysis and complex scenario resolution. Our architecture introduces three key innovations: (1) A dynamic switching mechanism enabling slow system intervention based on real-time uncertainty assessment; (2) An information bottleneck with high-level plan feedback that optimizes the slow system's guidance capability; (3) A bidirectional knowledge exchange where visual prompts enhance the slow system's reasoning while its feedback refines the fast planner's decision-making. To strengthen VLM reasoning, we develop a question-answering mechanism coupled with reward-instruct training strategy. In open-loop experiments, FASIONAD achieves a $6.7\%$ reduction in average $L2$ trajectory error and $28.1\%$ lower collision rate.

FASIONAD : FAst and Slow FusION Thinking Systems for Human-Like Autonomous Driving with Adaptive Feedback

Ensuring safe, comfortable, and efficient navigation is a critical goal for autonomous driving systems. While end-to-end models trained on large-scale datasets excel in common driving scenarios, they often struggle with rare, long-tail events. Recent progress in large language models (LLMs) has introduced enhanced reasoning capabilities, but their computational demands pose challenges for real-time decision-making and precise planning. This paper presents FASIONAD, a novel dual-system framework inspired by the cognitive model "Thinking, Fast and Slow." The fast system handles routine navigation tasks using rapid, data-driven path planning, while the slow system focuses on complex reasoning and decision-making in challenging or unfamiliar situations. A dynamic switching mechanism based on score distribution and feedback allows seamless transitions between the two systems. Visual prompts generated by the fast system enable human-like reasoning in the slow system, which provides high-quality feedback to enhance the fast system's decision-making. To evaluate FASIONAD, we introduce a new benchmark derived from the nuScenes dataset, specifically designed to differentiate fast and slow scenarios. FASIONAD achieves state-of-the-art performance on this benchmark, establishing a new standard for frameworks integrating fast and slow cognitive processes in autonomous driving. This approach paves the way for more adaptive, human-like autonomous driving systems.

From Laws to Motivation: Guiding Exploration through Law-Based Reasoning and Rewards

Large Language Models (LLMs) and Reinforcement Learning (RL) are two powerful approaches for building autonomous agents. However, due to limited understanding of the game environment, agents often resort to inefficient exploration and trial-and-error, struggling to develop long-term strategies or make decisions. We propose a method that extracts experience from interaction records to model the underlying laws of the game environment, using these experience as internal motivation to guide agents. These experience, expressed in language, are highly flexible and can either assist agents in reasoning directly or be transformed into rewards for guiding training. Our evaluation results in Crafter demonstrate that both RL and LLM agents benefit from these experience, leading to improved overall performance.

Equivariant score-based generative models provably learn distributions with symmetries efficiently

Symmetry is ubiquitous in many real-world phenomena and tasks, such as physics, images, and molecular simulations. Empirical studies have demonstrated that incorporating symmetries into generative models can provide better generalization and sampling efficiency when the underlying data distribution has group symmetry. In this work, we provide the first theoretical analysis and guarantees of score-based generative models (SGMs) for learning distributions that are invariant with respect to some group symmetry and offer the first quantitative comparison between data augmentation and adding equivariant inductive bias. First, building on recent works on the Wasserstein-1 ($\mathbf{d}_1$) guarantees of SGMs and empirical estimations of probability divergences under group symmetry, we provide an improved $\mathbf{d}_1$ generalization bound when the data distribution is group-invariant. Second, we describe the inductive bias of equivariant SGMs using Hamilton-Jacobi-Bellman theory, and rigorously demonstrate that one can learn the score of a symmetrized distribution using equivariant vector fields without data augmentations through the analysis of the optimality and equivalence of score-matching objectives. This also provides practical guidance that one does not have to augment the dataset as long as the vector field or the neural network parametrization is equivariant. Moreover, we quantify the impact of not incorporating equivariant structure into the score parametrization, by showing that non-equivariant vector fields can yield worse generalization bounds. This can be viewed as a type of model-form error that describes the missing structure of non-equivariant vector fields. Numerical simulations corroborate our analysis and highlight that data augmentations cannot replace the role of equivariant vector fields.

OmniRe: Omni Urban Scene Reconstruction

We introduce OmniRe, a holistic approach for efficiently reconstructing high-fidelity dynamic urban scenes from on-device logs. Recent methods for modeling driving sequences using neural radiance fields or Gaussian Splatting have demonstrated the potential of reconstructing challenging dynamic scenes, but often overlook pedestrians and other non-vehicle dynamic actors, hindering a complete pipeline for dynamic urban scene reconstruction. To that end, we propose a comprehensive 3DGS framework for driving scenes, named OmniRe, that allows for accurate, full-length reconstruction of diverse dynamic objects in a driving log. OmniRe builds dynamic neural scene graphs based on Gaussian representations and constructs multiple local canonical spaces that model various dynamic actors, including vehicles, pedestrians, and cyclists, among many others. This capability is unmatched by existing methods. OmniRe allows us to holistically reconstruct different objects present in the scene, subsequently enabling the simulation of reconstructed scenarios with all actors participating in real-time (~60Hz). Extensive evaluations on the Waymo dataset show that our approach outperforms prior state-of-the-art methods quantitatively and qualitatively by a large margin. We believe our work fills a critical gap in driving reconstruction.

Learning heavy-tailed distributions with Wasserstein-proximal-regularized $α$-divergences

In this paper, we propose Wasserstein proximals of $\alpha$-divergences as suitable objective functionals for learning heavy-tailed distributions in a stable manner. First, we provide sufficient, and in some cases necessary, relations among data dimension, $\alpha$, and the decay rate of data distributions for the Wasserstein-proximal-regularized divergence to be finite. Finite-sample convergence rates for the estimation in the case of the Wasserstein-1 proximal divergences are then provided under certain tail conditions. Numerical experiments demonstrate stable learning of heavy-tailed distributions -- even those without first or second moment -- without any explicit knowledge of the tail behavior, using suitable generative models such as GANs and flow-based models related to our proposed Wasserstein-proximal-regularized $\alpha$-divergences. Heuristically, $\alpha$-divergences handle the heavy tails and Wasserstein proximals allow non-absolute continuity between distributions and control the velocities of flow-based algorithms as they learn the target distribution deep into the tails.

360-Degree Panorama Generation from Few Unregistered NFoV Images

360$^\circ$ panoramas are extensively utilized as environmental light sources in computer graphics. However, capturing a 360$^\circ$ $\times$ 180$^\circ$ panorama poses challenges due to the necessity of specialized and costly equipment, and additional human resources. Prior studies develop various learning-based generative methods to synthesize panoramas from a single Narrow Field-of-View (NFoV) image, but they are limited in alterable input patterns, generation quality, and controllability. To address these issues, we propose a novel pipeline called PanoDiff, which efficiently generates complete 360$^\circ$ panoramas using one or more unregistered NFoV images captured from arbitrary angles. Our approach has two primary components to overcome the limitations. Firstly, a two-stage angle prediction module to handle various numbers of NFoV inputs. Secondly, a novel latent diffusion-based panorama generation model uses incomplete panorama and text prompts as control signals and utilizes several geometric augmentation schemes to ensure geometric properties in generated panoramas. Experiments show that PanoDiff achieves state-of-the-art panoramic generation quality and high controllability, making it suitable for applications such as content editing.