Stochastic Lifting for Generating Trajectories of Stochastic Physical Systems

Many stochastic physical systems evolve smoothly over time in the sense that the distribution of states changes regularly across time steps. The transition from current state to the next state can often be modeled as the combination of a smooth map and an explicit source of randomness. Stochastic Lifting exploits this structure by attaching an independent, high-dimensional random label to each state transition in the training data and fitting a transition map from the current state and label to the next state using a standard regression loss. The labels act as auxiliary coordinates that let the model represent multiple plausible next states from similar current states, avoiding collapse to a mean prediction in the finite-sample size regime. At inference, fresh labels are sampled at each time step and the learned map is rolled forward autoregressively, generating diverse trajectories with a single network evaluation per time step.

Two-Parameter Flows for Learning Population Dynamics of Physical Systems

This work addresses the problem of learning the dynamics of high-dimensional probability densities over time using unlabeled samples, without assuming access to trajectory information. We introduce two-parameter flows that learn only sampling-time transports from a base distribution to each marginal and then extract a physics-time velocity by regressing on coupled synthetic trajectories. We prove that the resulting physics-time dynamics are unique and inherit regularity from the sampling-time transports. Because we can build on standard, well-developed conditional flow matching techniques for learning the base-to-marginal transports, our approach scales to high dimensions and avoids per-step optimal-transport couplings, while allowing admissible non-gradient dynamics that can naturally explain rotational or circulating physics phenomena.

Leveraging Gauge Freedom for Learning Non-Gradient Population Dynamics of Stochastic Systems

Existing work on population dynamics inference often focuses on flows arising from vector fields that are the gradients of scalar potentials. Among all admissible flows that are compatible with the population dynamics, gradient flows are optimal in a specific sense: they minimize kinetic energy. The selection of fields based on different criteria corresponds to a gauge freedom when determining population dynamics, which we leverage in this work. We propose Non-Gradient Inference Flows (NGIF), an algorithm to infer non-gradient population dynamics using a weak formulation of the continuity equation. This allows us to parameterize general vector fields and choose other selection criteria beyond minimal kinetic energy. We demonstrate on a variety of low- and high-dimensional physics problems that this more general approach improves distributional accuracy over gradient-restricted baselines and better captures non-potential transport.

Parametric model reduction of mean-field and stochastic systems via higher-order action matching

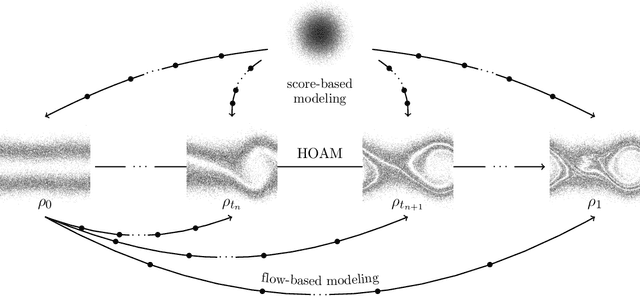
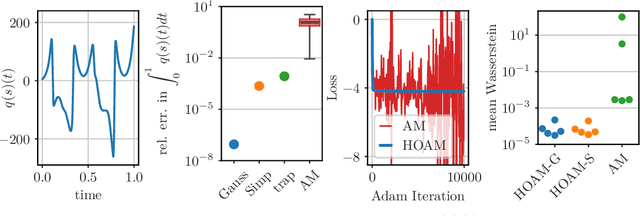
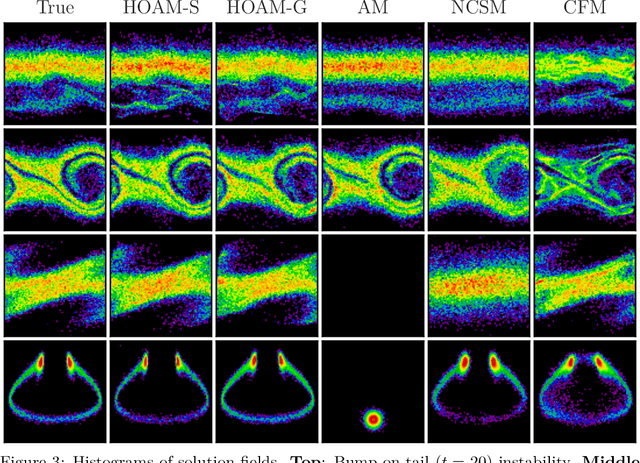
The aim of this work is to learn models of population dynamics of physical systems that feature stochastic and mean-field effects and that depend on physics parameters. The learned models can act as surrogates of classical numerical models to efficiently predict the system behavior over the physics parameters. Building on the Benamou-Brenier formula from optimal transport and action matching, we use a variational problem to infer parameter- and time-dependent gradient fields that represent approximations of the population dynamics. The inferred gradient fields can then be used to rapidly generate sample trajectories that mimic the dynamics of the physical system on a population level over varying physics parameters. We show that combining Monte Carlo sampling with higher-order quadrature rules is critical for accurately estimating the training objective from sample data and for stabilizing the training process. We demonstrate on Vlasov-Poisson instabilities as well as on high-dimensional particle and chaotic systems that our approach accurately predicts population dynamics over a wide range of parameters and outperforms state-of-the-art diffusion-based and flow-based modeling that simply condition on time and physics parameters.