Constraint-Based Regularization of Neural Networks
Paper and Code
Jun 17, 2020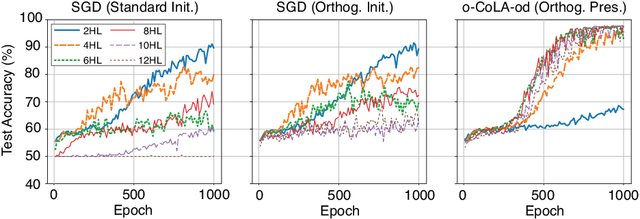


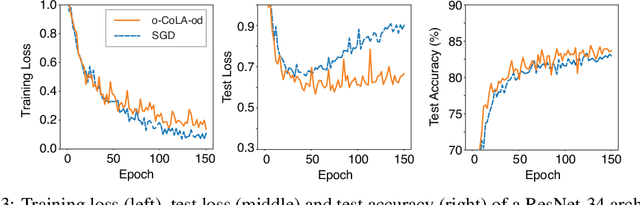
We propose a method for efficiently incorporating constraints into a stochastic gradient Langevin framework for the training of deep neural networks. Constraints allow direct control of the parameter space of the model. Appropriately designed, they reduce the vanishing/exploding gradient problem, control weight magnitudes and stabilize deep neural networks and thus improve the robustness of training algorithms and the generalization capabilities of the trained neural network. We present examples of constrained training methods motivated by orthogonality preservation for weight matrices and explicit weight normalizations. We describe the methods in the overdamped formulation of Langevin dynamics and the underdamped form, in which momenta help to improve sampling efficiency. The methods are explored in test examples in image classification and natural language processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge