Partitioned integrators for thermodynamic parameterization of neural networks

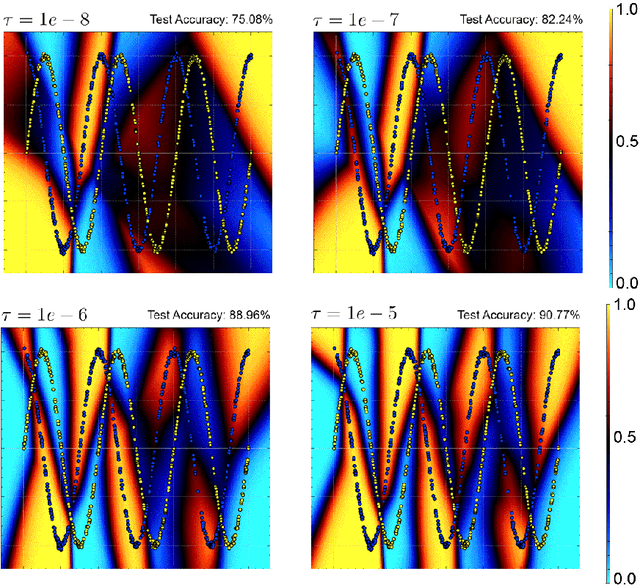
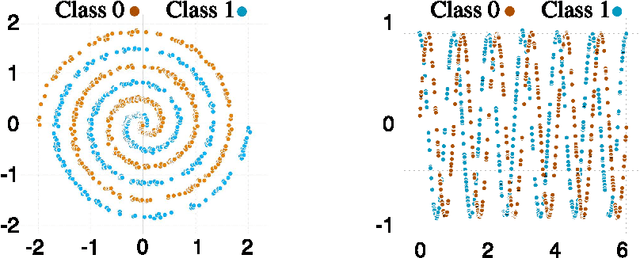
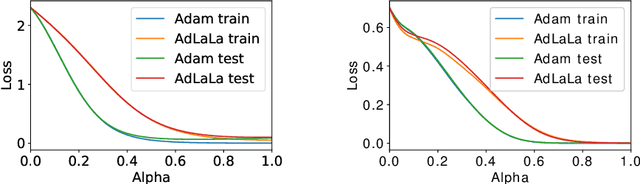
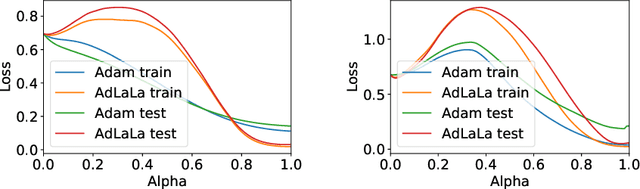
Stochastic Gradient Langevin Dynamics, the "unadjusted Langevin algorithm", and Adaptive Langevin Dynamics (also known as Stochastic Gradient Nos\'{e}-Hoover dynamics) are examples of existing thermodynamic parameterization methods in use for machine learning, but these can be substantially improved. We find that by partitioning the parameters based on natural layer structure we obtain schemes with rapid convergence for data sets with complicated loss landscapes. We describe easy-to-implement hybrid partitioned numerical algorithms, based on discretized stochastic differential equations, which are adapted to feed-forward neural networks, including LaLa (a multi-layer Langevin algorithm), AdLaLa (combining the adaptive Langevin and Langevin algorithms) and LOL (combining Langevin and Overdamped Langevin); we examine the convergence of these methods using numerical studies and compare their performance among themselves and in relation to standard alternatives such as stochastic gradient descent and ADAM. We present evidence that thermodynamic parameterization methods can be (i) faster, (ii) more accurate, and (iii) more robust than standard algorithms incorporated into machine learning frameworks, in particular for data sets with complicated loss landscapes. Moreover, we show in numerical studies that methods based on sampling excite many degrees of freedom. The equipartition property, which is a consequence of their ergodicity, means that these methods keep in play an ensemble of low-loss states during the training process. By drawing parameter states from a sufficiently rich distribution of nearby candidate states, we show that the thermodynamic schemes produce smoother classifiers, improve generalization and reduce overfitting compared to traditional optimizers.