Beam Search for Feature Selection

In this paper, we present and prove some consistency results about the performance of classification models using a subset of features. In addition, we propose to use beam search to perform feature selection, which can be viewed as a generalization of forward selection. We apply beam search to both simulated and real-world data, by evaluating and comparing the performance of different classification models using different sets of features. The results demonstrate that beam search could outperform forward selection, especially when the features are correlated so that they have more discriminative power when considered jointly than individually. Moreover, in some cases classification models could obtain comparable performance using only ten features selected by beam search instead of hundreds of original features.

Classification with Nearest Disjoint Centroids

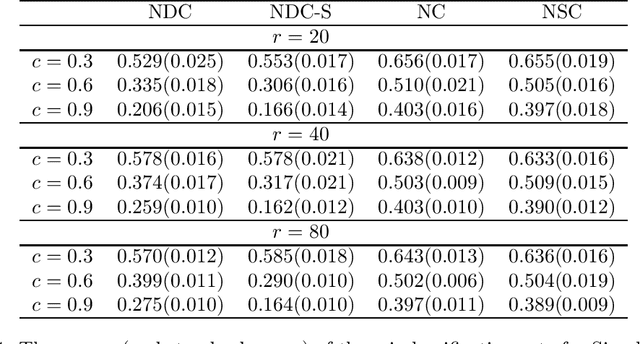
In this paper, we develop a new classification method based on nearest centroid, and it is called the nearest disjoint centroid classifier. Our method differs from the nearest centroid classifier in the following two aspects: (1) the centroids are defined based on disjoint subsets of features instead of all the features, and (2) the distance is induced by the dimensionality-normalized norm instead of the Euclidean norm. We provide a few theoretical results regarding our method. In addition, we propose a simple algorithm based on adapted k-means clustering that can find the disjoint subsets of features used in our method, and extend the algorithm to perform feature selection. We evaluate and compare the performance of our method to other closely related classifiers on both simulated data and real-world gene expression datasets. The results demonstrate that our method is able to outperform other competing classifiers by having smaller misclassification rates and/or using fewer features in various settings and situations.

Biclustering with Alternating K-Means

Biclustering is the task of simultaneously clustering the rows and columns of the data matrix into different subgroups such that the rows and columns within a subgroup exhibit similar patterns. In this paper, we consider the case of producing exclusive row and column biclusters. We provide a new formulation of the biclustering problem based on the idea of minimizing the empirical clustering risk. We develop and prove a consistency result with respect to the empirical clustering risk. Since the optimization problem is combinatorial in nature, finding the global minimum is computationally intractable. In light of this fact, we propose a simple and novel algorithm that finds a local minimum by alternating the use of an adapted version of the k-means clustering algorithm between columns and rows. We evaluate and compare the performance of our algorithm to other related biclustering methods on both simulated data and real-world gene expression data sets. The results demonstrate that our algorithm is able to detect meaningful structures in the data and outperform other competing biclustering methods in various settings and situations.

A metric on directed graphs and Markov chains based on hitting probabilities

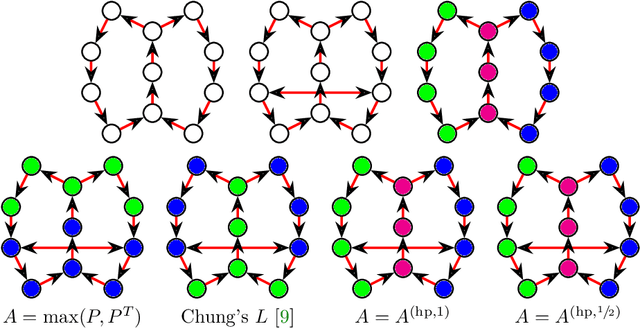
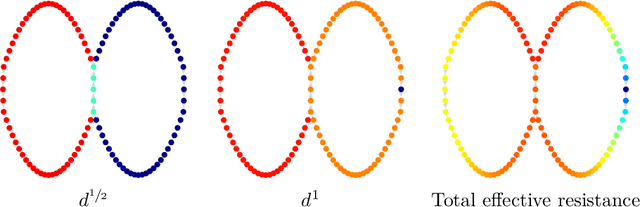
The shortest-path, commute time, and diffusion distances on undirected graphs have been widely employed in applications such as dimensionality reduction, link prediction, and trip planning. Increasingly, there is interest in using asymmetric structure of data derived from Markov chains and directed graphs, but few metrics are specifically adapted to this task. We introduce a metric on the state space of any ergodic, finite-state, time-homogeneous Markov chain and, in particular, on any Markov chain derived from a directed graph. Our construction is based on hitting probabilities, with nearness in the metric space related to the transfer of random walkers from one node to another at stationarity. Notably, our metric is insensitive to shortest and average path distances, thus giving new information compared to existing metrics. We use possible degeneracies in the metric to develop an interesting structural theory of directed graphs and explore a related quotienting procedure. Our metric can be computed in $O(n^3)$ time, where $n$ is the number of states, and in examples we scale up to $n=10,000$ nodes and $\approx 38M$ edges on a desktop computer. In several examples, we explore the nature of the metric, compare it to alternative methods, and demonstrate its utility for weak recovery of community structure in dense graphs, visualization, structure recovering, dynamics exploration, and multiscale cluster detection.