Wasserstein Archetypal Analysis

Archetypal analysis is an unsupervised machine learning method that summarizes data using a convex polytope. In its original formulation, for fixed k, the method finds a convex polytope with k vertices, called archetype points, such that the polytope is contained in the convex hull of the data and the mean squared Euclidean distance between the data and the polytope is minimal. In the present work, we consider an alternative formulation of archetypal analysis based on the Wasserstein metric, which we call Wasserstein archetypal analysis (WAA). In one dimension, there exists a unique solution of WAA and, in two dimensions, we prove existence of a solution, as long as the data distribution is absolutely continuous with respect to Lebesgue measure. We discuss obstacles to extending our result to higher dimensions and general data distributions. We then introduce an appropriate regularization of the problem, via a Renyi entropy, which allows us to obtain existence of solutions of the regularized problem for general data distributions, in arbitrary dimensions. We prove a consistency result for the regularized problem, ensuring that if the data are iid samples from a probability measure, then as the number of samples is increased, a subsequence of the archetype points converges to the archetype points for the limiting data distribution, almost surely. Finally, we develop and implement a gradient-based computational approach for the two-dimensional problem, based on the semi-discrete formulation of the Wasserstein metric. Our analysis is supported by detailed computational experiments.

A dynamical systems based framework for dimension reduction

We propose a novel framework for learning a low-dimensional representation of data based on nonlinear dynamical systems, which we call dynamical dimension reduction (DDR). In the DDR model, each point is evolved via a nonlinear flow towards a lower-dimensional subspace; the projection onto the subspace gives the low-dimensional embedding. Training the model involves identifying the nonlinear flow and the subspace. Following the equation discovery method, we represent the vector field that defines the flow using a linear combination of dictionary elements, where each element is a pre-specified linear/nonlinear candidate function. A regularization term for the average total kinetic energy is also introduced and motivated by optimal transport theory. We prove that the resulting optimization problem is well-posed and establish several properties of the DDR method. We also show how the DDR method can be trained using a gradient-based optimization method, where the gradients are computed using the adjoint method from optimal control theory. The DDR method is implemented and compared on synthetic and example datasets to other dimension reductions methods, including PCA, t-SNE, and Umap.

Probabilistic methods for approximate archetypal analysis

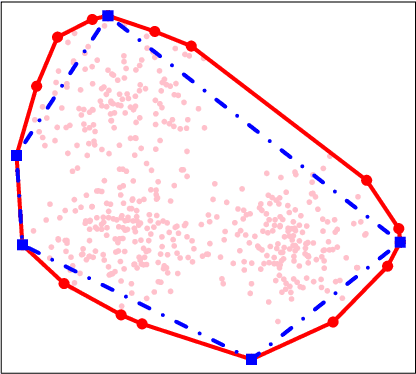
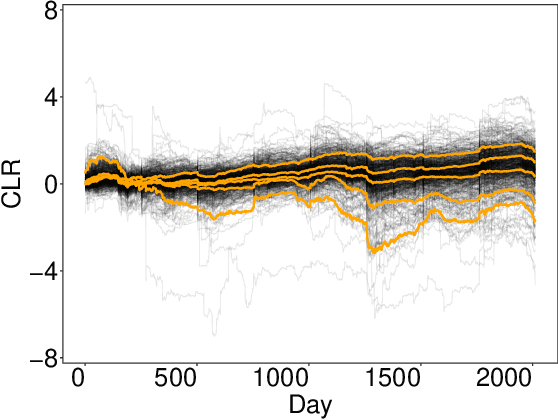
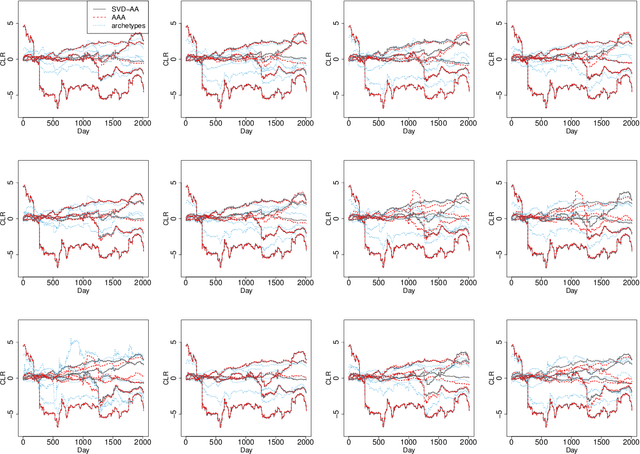
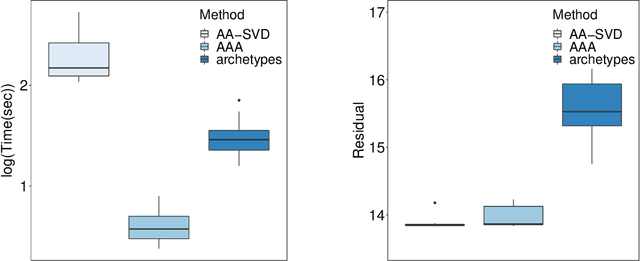
Archetypal analysis is an unsupervised learning method for exploratory data analysis. One major challenge that limits the applicability of archetypal analysis in practice is the inherent computational complexity of the existing algorithms. In this paper, we provide a novel approximation approach to partially address this issue. Utilizing probabilistic ideas from high-dimensional geometry, we introduce two preprocessing techniques to reduce the dimension and representation cardinality of the data, respectively. We prove that, provided the data is approximately embedded in a low-dimensional linear subspace and the convex hull of the corresponding representations is well approximated by a polytope with a few vertices, our method can effectively reduce the scaling of archetypal analysis. Moreover, the solution of the reduced problem is near-optimal in terms of prediction errors. Our approach can be combined with other acceleration techniques to further mitigate the intrinsic complexity of archetypal analysis. We demonstrate the usefulness of our results by applying our method to summarize several moderately large-scale datasets.

A non-autonomous equation discovery method for time signal classification

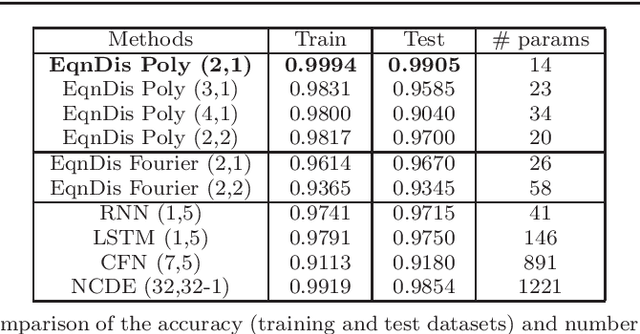
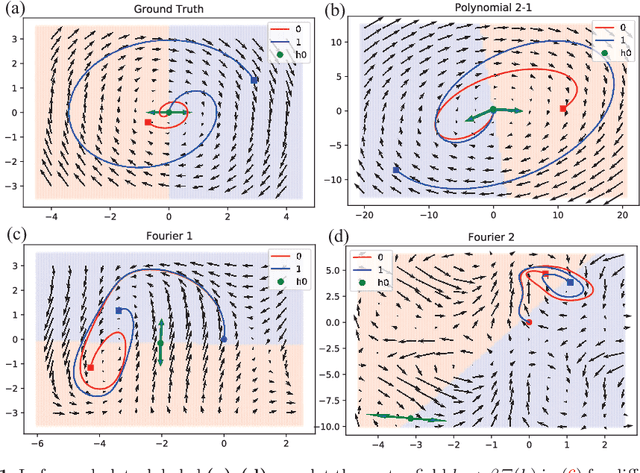
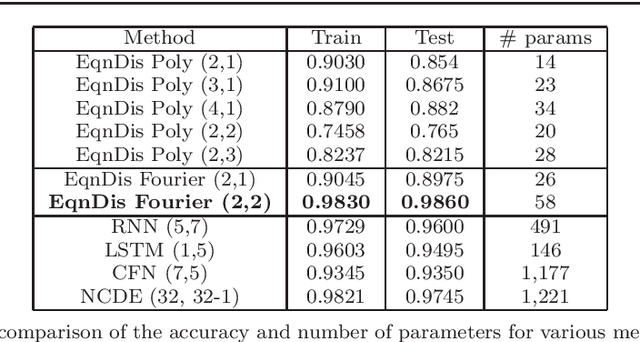
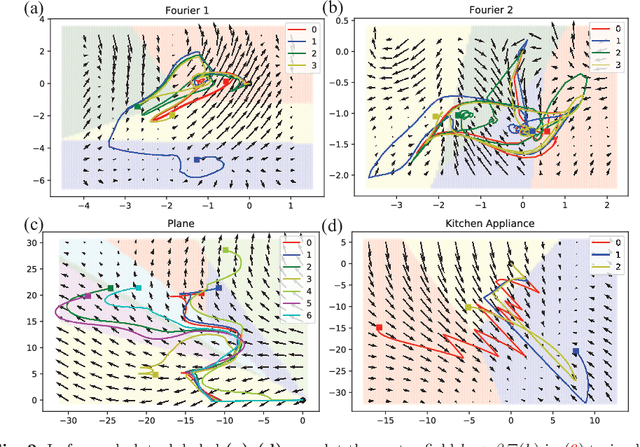
Certain neural network architectures, in the infinite-layer limit, lead to systems of nonlinear differential equations. Motivated by this idea, we develop a framework for analyzing time signals based on non-autonomous dynamical equations. We view the time signal as a forcing function for a dynamical system that governs a time-evolving hidden variable. As in equation discovery, the dynamical system is represented using a dictionary of functions and the coefficients are learned from data. This framework is applied to the time signal classification problem. We show how gradients can be efficiently computed using the adjoint method, and we apply methods from dynamical systems to establish stability of the classifier. Through a variety of experiments, on both synthetic and real datasets, we show that the proposed method uses orders of magnitude fewer parameters than competing methods, while achieving comparable accuracy. We created the synthetic datasets using dynamical systems of increasing complexity; though the ground truth vector fields are often polynomials, we find consistently that a Fourier dictionary yields the best results. We also demonstrate how the proposed method yields graphical interpretability in the form of phase portraits.

Consistency of archetypal analysis

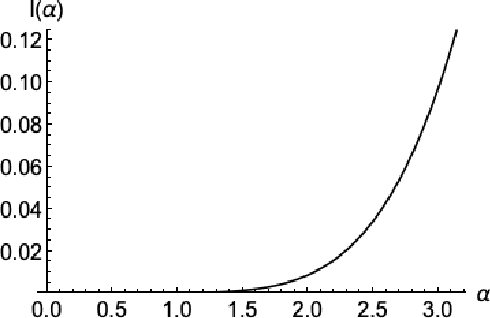
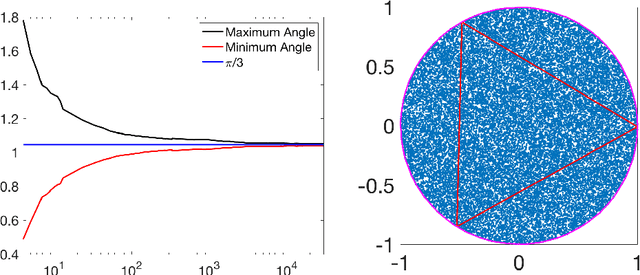
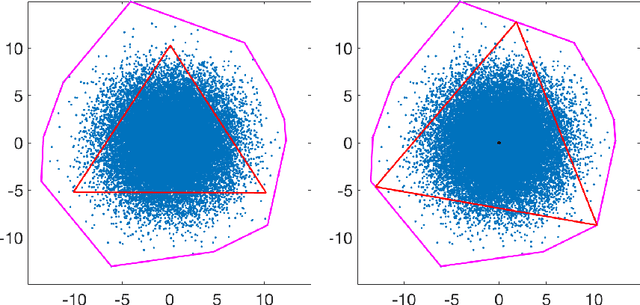
Archetypal analysis is an unsupervised learning method that uses a convex polytope to summarize multivariate data. For fixed $k$, the method finds a convex polytope with $k$ vertices, called archetype points, such that the polytope is contained in the convex hull of the data and the mean squared distance between the data and the polytope is minimal. In this paper, we prove a consistency result that shows if the data is independently sampled from a probability measure with bounded support, then the archetype points converge to a solution of the continuum version of the problem, of which we identify and establish several properties. We also obtain the convergence rate of the optimal objective values under appropriate assumptions on the distribution. If the data is independently sampled from a distribution with unbounded support, we also prove a consistency result for a modified method that penalizes the dispersion of the archetype points. Our analysis is supported by detailed computational experiments of the archetype points for data sampled from the uniform distribution in a disk, the normal distribution, an annular distribution, and a Gaussian mixture model.

A metric on directed graphs and Markov chains based on hitting probabilities

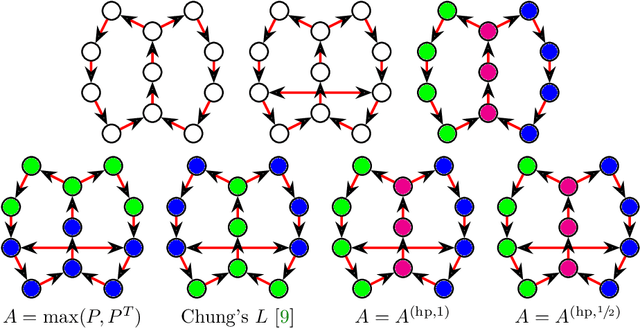
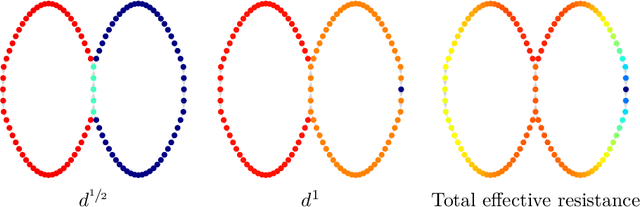
The shortest-path, commute time, and diffusion distances on undirected graphs have been widely employed in applications such as dimensionality reduction, link prediction, and trip planning. Increasingly, there is interest in using asymmetric structure of data derived from Markov chains and directed graphs, but few metrics are specifically adapted to this task. We introduce a metric on the state space of any ergodic, finite-state, time-homogeneous Markov chain and, in particular, on any Markov chain derived from a directed graph. Our construction is based on hitting probabilities, with nearness in the metric space related to the transfer of random walkers from one node to another at stationarity. Notably, our metric is insensitive to shortest and average path distances, thus giving new information compared to existing metrics. We use possible degeneracies in the metric to develop an interesting structural theory of directed graphs and explore a related quotienting procedure. Our metric can be computed in $O(n^3)$ time, where $n$ is the number of states, and in examples we scale up to $n=10,000$ nodes and $\approx 38M$ edges on a desktop computer. In several examples, we explore the nature of the metric, compare it to alternative methods, and demonstrate its utility for weak recovery of community structure in dense graphs, visualization, structure recovering, dynamics exploration, and multiscale cluster detection.

A continuum limit for the PageRank algorithm

Semi-supervised and unsupervised machine learning methods often rely on graphs to model data, prompting research on how theoretical properties of operators on graphs are leveraged in learning problems. While most of the existing literature focuses on undirected graphs, directed graphs are very important in practice, giving models for physical, biological, or transportation networks, among many other applications. In this paper, we propose a new framework for rigorously studying continuum limits of learning algorithms on directed graphs. We use the new framework to study the PageRank algorithm, and show how it can be interpreted as a numerical scheme on a directed graph involving a type of normalized graph Laplacian. We show that the corresponding continuum limit problem, which is taken as the number of webpages grows to infinity, is a second-order, possibly degenerate, elliptic equation that contains reaction, diffusion, and advection terms. We prove that the numerical scheme is consistent and stable and compute explicit rates of convergence of the discrete solution to the solution of the continuum limit PDE. We give applications to proving stability and asymptotic regularity of the PageRank vector.

Consistency of Dirichlet Partitions

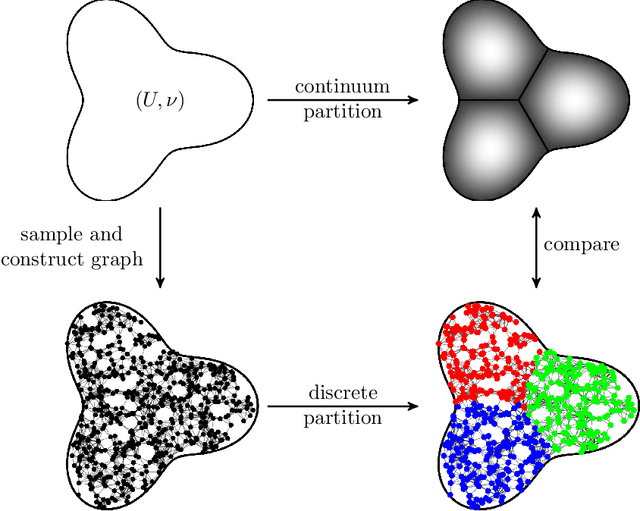
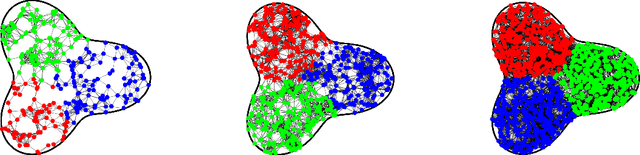
A Dirichlet $k$-partition of a domain $U \subseteq \mathbb{R}^d$ is a collection of $k$ pairwise disjoint open subsets such that the sum of their first Laplace-Dirichlet eigenvalues is minimal. A discrete version of Dirichlet partitions has been posed on graphs with applications in data analysis. Both versions admit variational formulations: solutions are characterized by minimizers of the Dirichlet energy of mappings from $U$ into a singular space $\Sigma_k \subseteq \mathbb{R}^k$. In this paper, we extend results of N.\ Garc\'ia Trillos and D.\ Slep\v{c}ev to show that there exist solutions of the continuum problem arising as limits to solutions of a sequence of discrete problems. Specifically, a sequence of points $\{x_i\}_{i \in \mathbb{N}}$ from $U$ is sampled i.i.d.\ with respect to a given probability measure $\nu$ on $U$ and for all $n \in \mathbb{N}$, a geometric graph $G_n$ is constructed from the first $n$ points $x_1, x_2, \ldots, x_n$ and the pairwise distances between the points. With probability one with respect to the choice of points $\{x_i\}_{i \in \mathbb{N}}$, we show that as $n \to \infty$ the discrete Dirichlet energies for functions $G_n \to \Sigma_k$ $\Gamma$-converge to (a scalar multiple of) the continuum Dirichlet energy for functions $U \to \Sigma_k$ with respect to a metric coming from the theory of optimal transport. This, along with a compactness property for the aforementioned energies that we prove, implies the convergence of minimizers. When $\nu$ is the uniform distribution, our results also imply the statistical consistency statement that Dirichlet partitions of geometric graphs converge to partitions of the sampled space in the Hausdorff sense.

Analysis of Crowdsourced Sampling Strategies for HodgeRank with Sparse Random Graphs

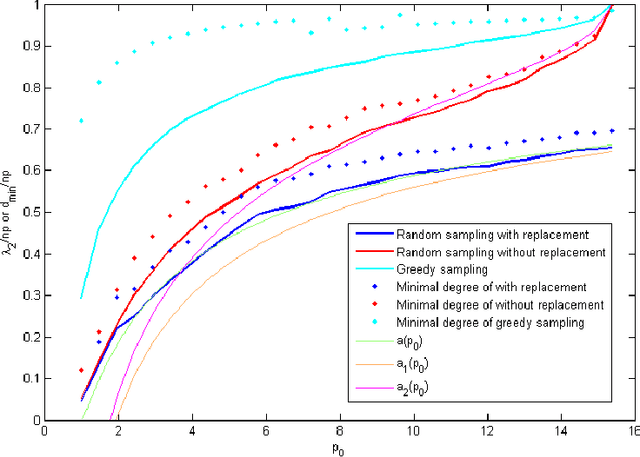
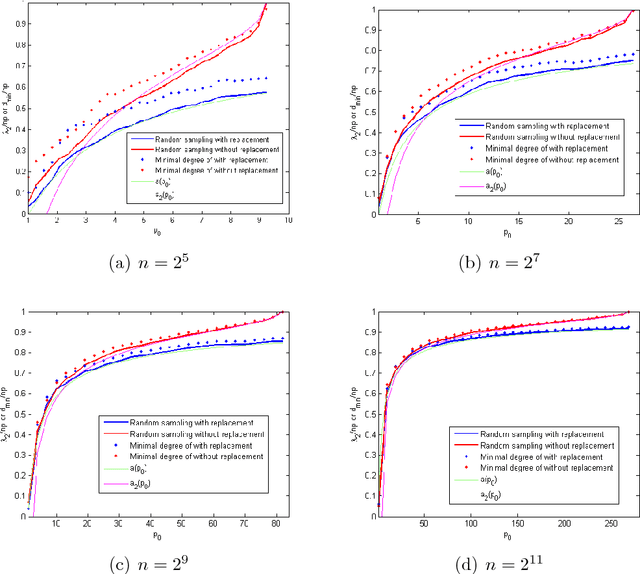
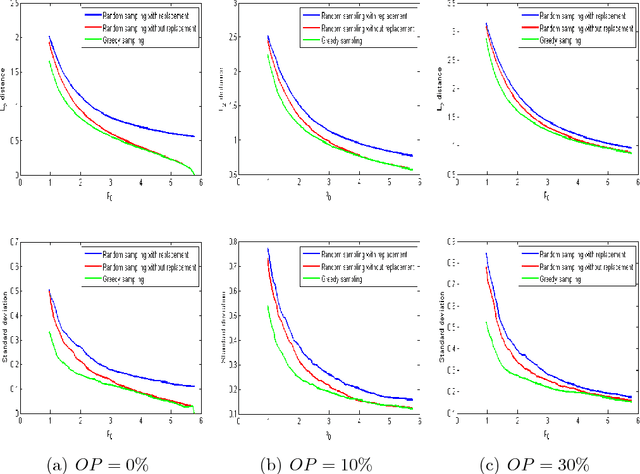
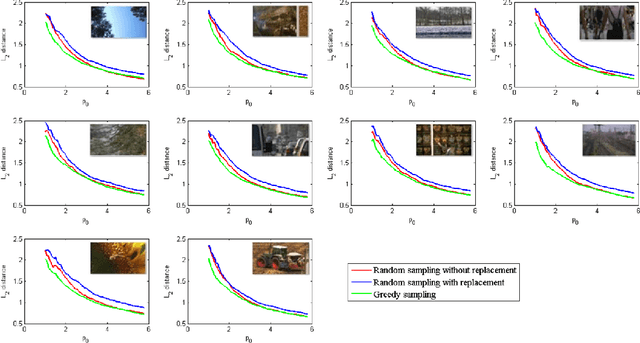
Crowdsourcing platforms are now extensively used for conducting subjective pairwise comparison studies. In this setting, a pairwise comparison dataset is typically gathered via random sampling, either \emph{with} or \emph{without} replacement. In this paper, we use tools from random graph theory to analyze these two random sampling methods for the HodgeRank estimator. Using the Fiedler value of the graph as a measurement for estimator stability (informativeness), we provide a new estimate of the Fiedler value for these two random graph models. In the asymptotic limit as the number of vertices tends to infinity, we prove the validity of the estimate. Based on our findings, for a small number of items to be compared, we recommend a two-stage sampling strategy where a greedy sampling method is used initially and random sampling \emph{without} replacement is used in the second stage. When a large number of items is to be compared, we recommend random sampling with replacement as this is computationally inexpensive and trivially parallelizable. Experiments on synthetic and real-world datasets support our analysis.

Optimal Data Collection For Informative Rankings Expose Well-Connected Graphs

Given a graph where vertices represent alternatives and arcs represent pairwise comparison data, the statistical ranking problem is to find a potential function, defined on the vertices, such that the gradient of the potential function agrees with the pairwise comparisons. Our goal in this paper is to develop a method for collecting data for which the least squares estimator for the ranking problem has maximal Fisher information. Our approach, based on experimental design, is to view data collection as a bi-level optimization problem where the inner problem is the ranking problem and the outer problem is to identify data which maximizes the informativeness of the ranking. Under certain assumptions, the data collection problem decouples, reducing to a problem of finding multigraphs with large algebraic connectivity. This reduction of the data collection problem to graph-theoretic questions is one of the primary contributions of this work. As an application, we study the Yahoo! Movie user rating dataset and demonstrate that the addition of a small number of well-chosen pairwise comparisons can significantly increase the Fisher informativeness of the ranking. As another application, we study the 2011-12 NCAA football schedule and propose schedules with the same number of games which are significantly more informative. Using spectral clustering methods to identify highly-connected communities within the division, we argue that the NCAA could improve its notoriously poor rankings by simply scheduling more out-of-conference games.