Todd Harry Reeb
Consistency of Dirichlet Partitions
Aug 18, 2017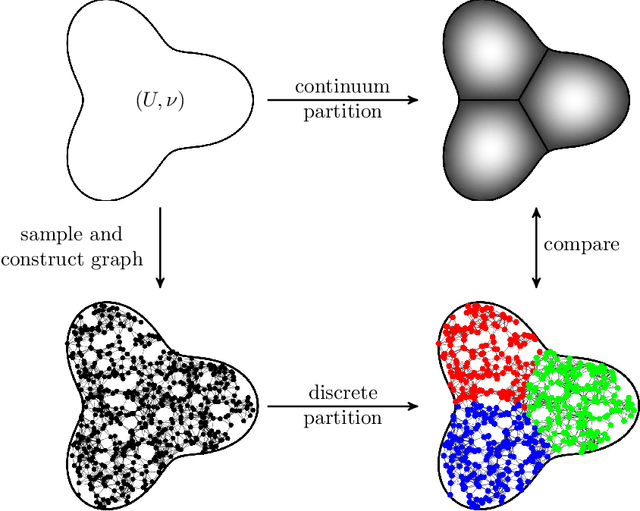
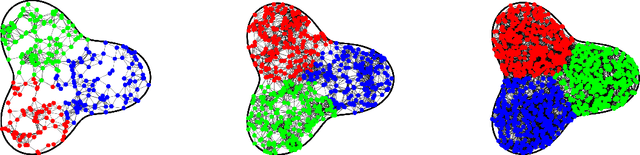

Abstract:A Dirichlet $k$-partition of a domain $U \subseteq \mathbb{R}^d$ is a collection of $k$ pairwise disjoint open subsets such that the sum of their first Laplace-Dirichlet eigenvalues is minimal. A discrete version of Dirichlet partitions has been posed on graphs with applications in data analysis. Both versions admit variational formulations: solutions are characterized by minimizers of the Dirichlet energy of mappings from $U$ into a singular space $\Sigma_k \subseteq \mathbb{R}^k$. In this paper, we extend results of N.\ Garc\'ia Trillos and D.\ Slep\v{c}ev to show that there exist solutions of the continuum problem arising as limits to solutions of a sequence of discrete problems. Specifically, a sequence of points $\{x_i\}_{i \in \mathbb{N}}$ from $U$ is sampled i.i.d.\ with respect to a given probability measure $\nu$ on $U$ and for all $n \in \mathbb{N}$, a geometric graph $G_n$ is constructed from the first $n$ points $x_1, x_2, \ldots, x_n$ and the pairwise distances between the points. With probability one with respect to the choice of points $\{x_i\}_{i \in \mathbb{N}}$, we show that as $n \to \infty$ the discrete Dirichlet energies for functions $G_n \to \Sigma_k$ $\Gamma$-converge to (a scalar multiple of) the continuum Dirichlet energy for functions $U \to \Sigma_k$ with respect to a metric coming from the theory of optimal transport. This, along with a compactness property for the aforementioned energies that we prove, implies the convergence of minimizers. When $\nu$ is the uniform distribution, our results also imply the statistical consistency statement that Dirichlet partitions of geometric graphs converge to partitions of the sampled space in the Hausdorff sense.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge