A metric on directed graphs and Markov chains based on hitting probabilities

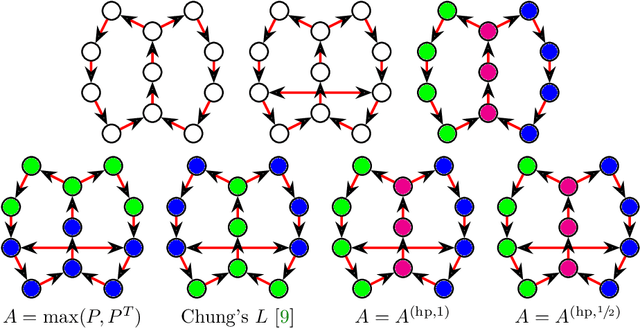
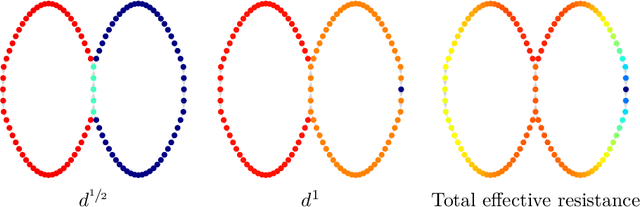
The shortest-path, commute time, and diffusion distances on undirected graphs have been widely employed in applications such as dimensionality reduction, link prediction, and trip planning. Increasingly, there is interest in using asymmetric structure of data derived from Markov chains and directed graphs, but few metrics are specifically adapted to this task. We introduce a metric on the state space of any ergodic, finite-state, time-homogeneous Markov chain and, in particular, on any Markov chain derived from a directed graph. Our construction is based on hitting probabilities, with nearness in the metric space related to the transfer of random walkers from one node to another at stationarity. Notably, our metric is insensitive to shortest and average path distances, thus giving new information compared to existing metrics. We use possible degeneracies in the metric to develop an interesting structural theory of directed graphs and explore a related quotienting procedure. Our metric can be computed in $O(n^3)$ time, where $n$ is the number of states, and in examples we scale up to $n=10,000$ nodes and $\approx 38M$ edges on a desktop computer. In several examples, we explore the nature of the metric, compare it to alternative methods, and demonstrate its utility for weak recovery of community structure in dense graphs, visualization, structure recovering, dynamics exploration, and multiscale cluster detection.

Stochastic Block Models are a Discrete Surface Tension

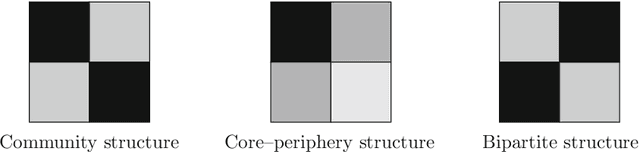
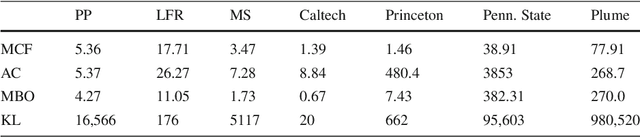
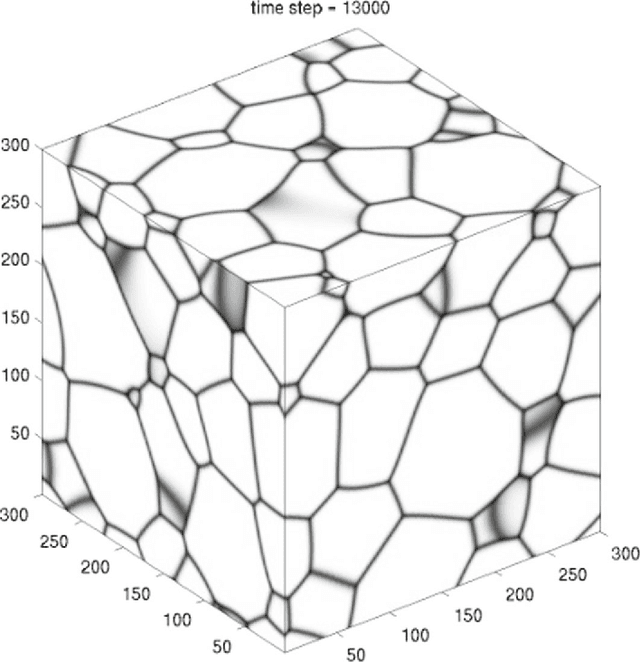
Networks, which represent agents and interactions between them, arise in myriad applications throughout the sciences, engineering, and even the humanities. To understand large-scale structure in a network, a common task is to cluster a network's nodes into sets called "communities" such that there are dense connections within communities but sparse connections between them. A popular and statistically principled method to perform such clustering is to use a family of generative models known as stochastic block models (SBMs). In this paper, we show that maximum likelihood estimation in an SBM is a network analog of a well-known continuum surface-tension problem that arises from an application in metallurgy. To illustrate the utility of this bridge, we implement network analogs of three surface-tension algorithms, with which we successfully recover planted community structure in synthetic networks and which yield fascinating insights on empirical networks from the field of hyperspectral video segmentation.