One Node at a Time: Node-Level Network Classification

Network classification aims to group networks (or graphs) into distinct categories based on their structure. We study the connection between classification of a network and of its constituent nodes, and whether nodes from networks in different groups are distinguishable based on structural node characteristics such as centrality and clustering coefficient. We demonstrate, using various network datasets and random network models, that a classifier can be trained to accurately predict the network category of a given node (without seeing the whole network), implying that complex networks display distinct structural patterns even at the node level. Finally, we discuss two applications of node-level network classification: (i) whole-network classification from small samples of nodes, and (ii) network bootstrapping.

A metric on directed graphs and Markov chains based on hitting probabilities

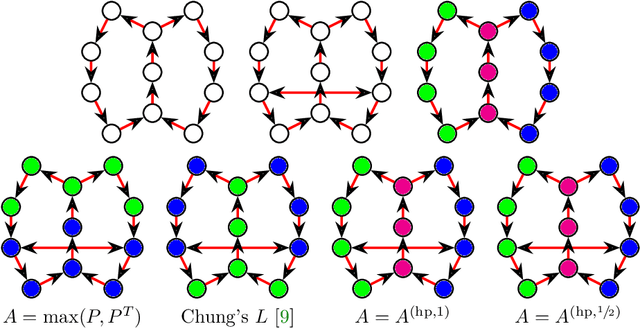
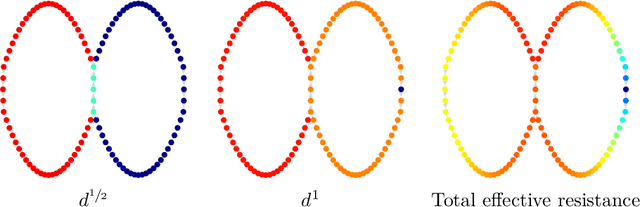
The shortest-path, commute time, and diffusion distances on undirected graphs have been widely employed in applications such as dimensionality reduction, link prediction, and trip planning. Increasingly, there is interest in using asymmetric structure of data derived from Markov chains and directed graphs, but few metrics are specifically adapted to this task. We introduce a metric on the state space of any ergodic, finite-state, time-homogeneous Markov chain and, in particular, on any Markov chain derived from a directed graph. Our construction is based on hitting probabilities, with nearness in the metric space related to the transfer of random walkers from one node to another at stationarity. Notably, our metric is insensitive to shortest and average path distances, thus giving new information compared to existing metrics. We use possible degeneracies in the metric to develop an interesting structural theory of directed graphs and explore a related quotienting procedure. Our metric can be computed in $O(n^3)$ time, where $n$ is the number of states, and in examples we scale up to $n=10,000$ nodes and $\approx 38M$ edges on a desktop computer. In several examples, we explore the nature of the metric, compare it to alternative methods, and demonstrate its utility for weak recovery of community structure in dense graphs, visualization, structure recovering, dynamics exploration, and multiscale cluster detection.

A Map Equation with Metadata: Varying the Role of Attributes in Community Detection

As the No Free Lunch theorem formally states [1], algorithms for detecting communities in networks must make tradeoffs. In this work, we present a method for using metadata to inform tradeoff decisions. We extend the content map equation, which adds metadata entropy to the traditional map equation, by introducing a tuning parameter allowing for explicit specification of the metadata's relative importance in assigning community labels. On synthetic networks, we show how tuning for node metadata relates to the detectability limit, and on empirical networks, we show how increased tuning for node metadata yields increased mutual information with the metadata at a cost in the traditional map equation. Our tuning parameter, like the focusing knob of a microscope, allows users to "zoom in" and "zoom out" on communities with varying levels of focus on the metadata.

Stochastic Block Models with Multiple Continuous Attributes

The stochastic block model (SBM) is a probabilistic model for community structure in networks. Typically, only the adjacency matrix is used to perform SBM parameter inference. In this paper, we consider circumstances in which nodes have an associated vector of continuous attributes that are also used to learn the node-to-community assignments and corresponding SBM parameters. While this assumption is not realistic for every application, our model assumes that the attributes associated with the nodes in a network's community can be described by a common multivariate Gaussian model. In this augmented, attributed SBM, the objective is to simultaneously learn the SBM connectivity probabilities with the multivariate Gaussian parameters describing each community. While there are recent examples in the literature that combine connectivity and attribute information to inform community detection, our model is the first augmented stochastic block model to handle multiple continuous attributes. This provides the flexibility in biological data to, for example, augment connectivity information with continuous measurements from multiple experimental modalities. Because the lack of labeled network data often makes community detection results difficult to validate, we highlight the usefulness of our model for two network prediction tasks: link prediction and collaborative filtering. As a result of fitting this attributed stochastic block model, one can predict the attribute vector or connectivity patterns for a new node in the event of the complementary source of information (connectivity or attributes, respectively). We also highlight two biological examples where the attributed stochastic block model provides satisfactory performance in the link prediction and collaborative filtering tasks.

Clustering Network Layers With the Strata Multilayer Stochastic Block Model

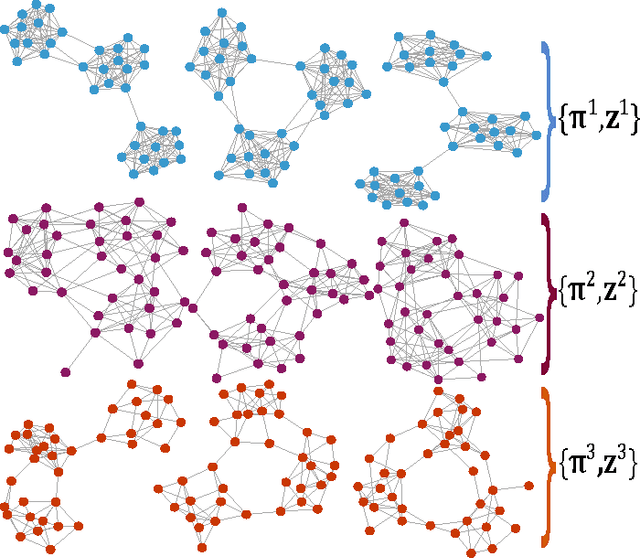
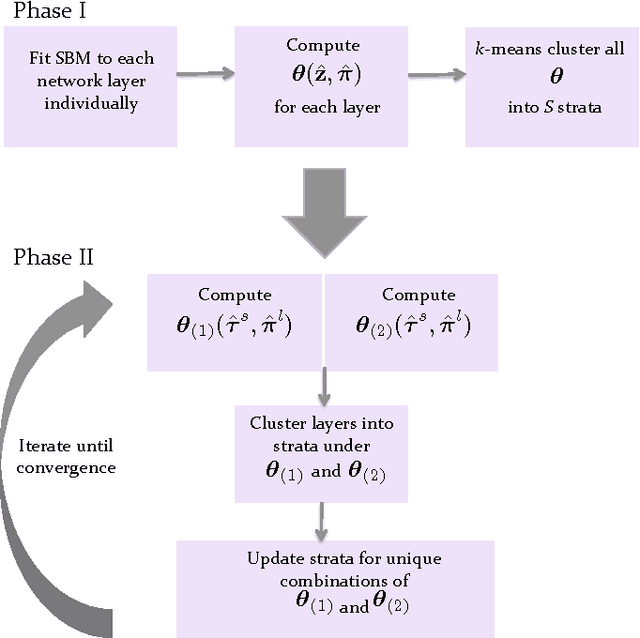
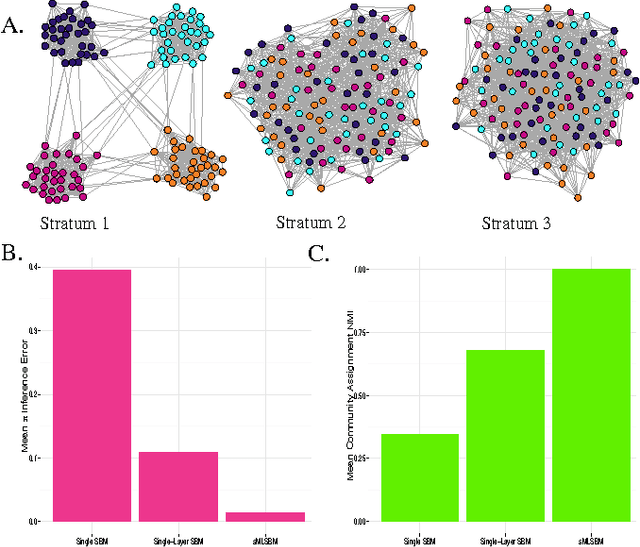
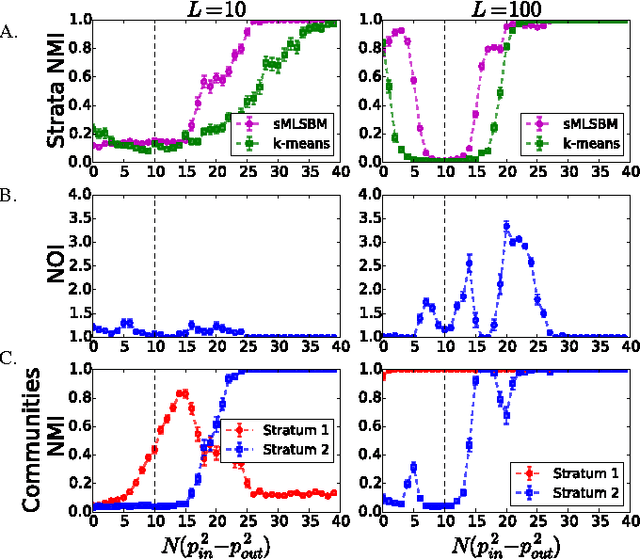
Multilayer networks are a useful data structure for simultaneously capturing multiple types of relationships between a set of nodes. In such networks, each relational definition gives rise to a layer. While each layer provides its own set of information, community structure across layers can be collectively utilized to discover and quantify underlying relational patterns between nodes. To concisely extract information from a multilayer network, we propose to identify and combine sets of layers with meaningful similarities in community structure. In this paper, we describe the "strata multilayer stochastic block model'' (sMLSBM), a probabilistic model for multilayer community structure. The central extension of the model is that there exist groups of layers, called "strata'', which are defined such that all layers in a given stratum have community structure described by a common stochastic block model (SBM). That is, layers in a stratum exhibit similar node-to-community assignments and SBM probability parameters. Fitting the sMLSBM to a multilayer network provides a joint clustering that yields node-to-community and layer-to-stratum assignments, which cooperatively aid one another during inference. We describe an algorithm for separating layers into their appropriate strata and an inference technique for estimating the SBM parameters for each stratum. We demonstrate our method using synthetic networks and a multilayer network inferred from data collected in the Human Microbiome Project.