The role of alcohol outlet visits derived from mobile phone location data in enhancing domestic violence prediction at the neighborhood level

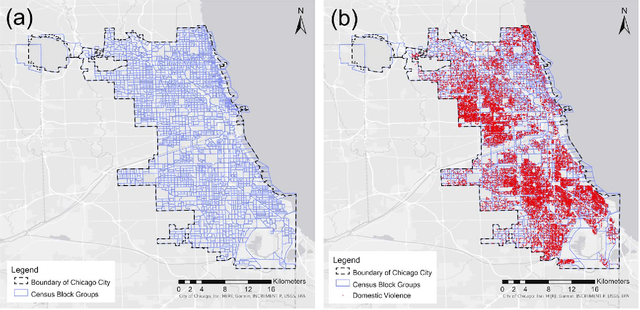
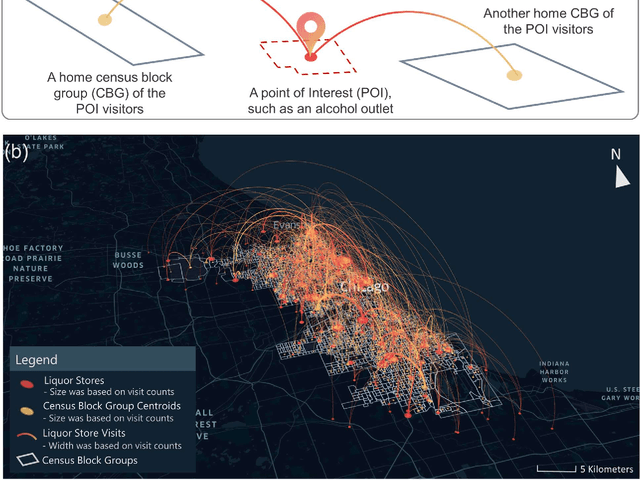
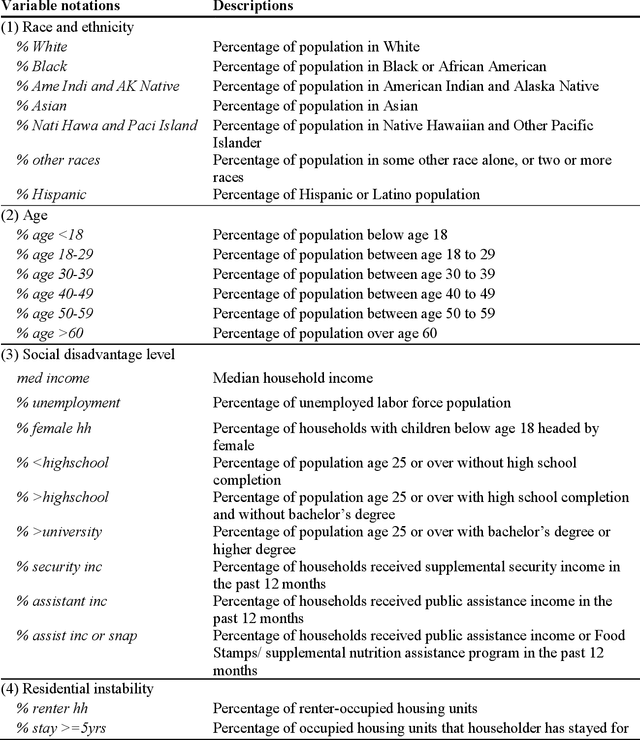
Domestic violence (DV) is a serious public health issue, with 1 in 3 women and 1 in 4 men experiencing some form of partner-related violence every year. Existing research has shown a strong association between alcohol use and DV at the individual level. Accordingly, alcohol use could also be a predictor for DV at the neighborhood level, helping identify the neighborhoods where DV is more likely to happen. However, it is difficult and costly to collect data that can represent neighborhood-level alcohol use especially for a large geographic area. In this study, we propose to derive information about the alcohol outlet visits of the residents of different neighborhoods from anonymized mobile phone location data, and investigate whether the derived visits can help better predict DV at the neighborhood level. We use mobile phone data from the company SafeGraph, which is freely available to researchers and which contains information about how people visit various points-of-interest including alcohol outlets. In such data, a visit to an alcohol outlet is identified based on the GPS point location of the mobile phone and the building footprint (a polygon) of the alcohol outlet. We present our method for deriving neighborhood-level alcohol outlet visits, and experiment with four different statistical and machine learning models to investigate the role of the derived visits in enhancing DV prediction based on an empirical dataset about DV in Chicago. Our results reveal the effectiveness of the derived alcohol outlets visits in helping identify neighborhoods that are more likely to suffer from DV, and can inform policies related to DV intervention and alcohol outlet licensing.

Impact of Community Structure on Consensus Machine Learning

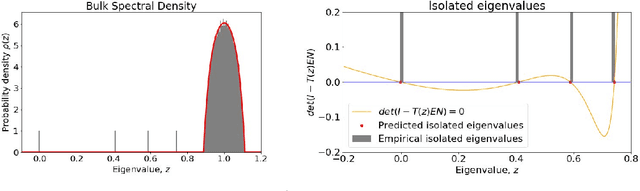
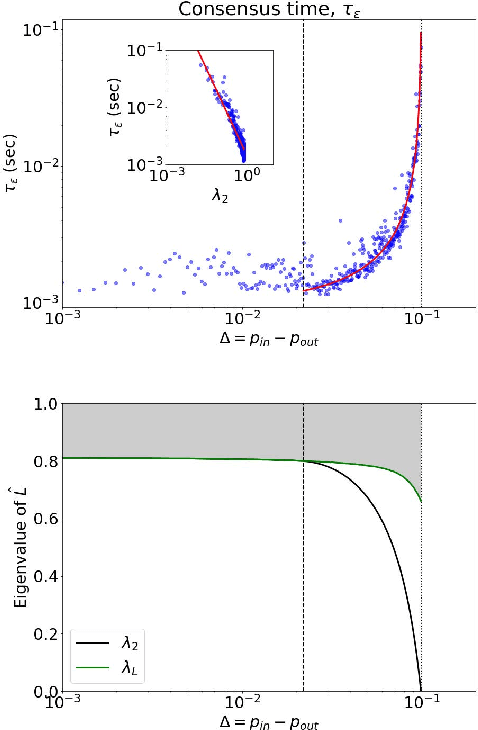
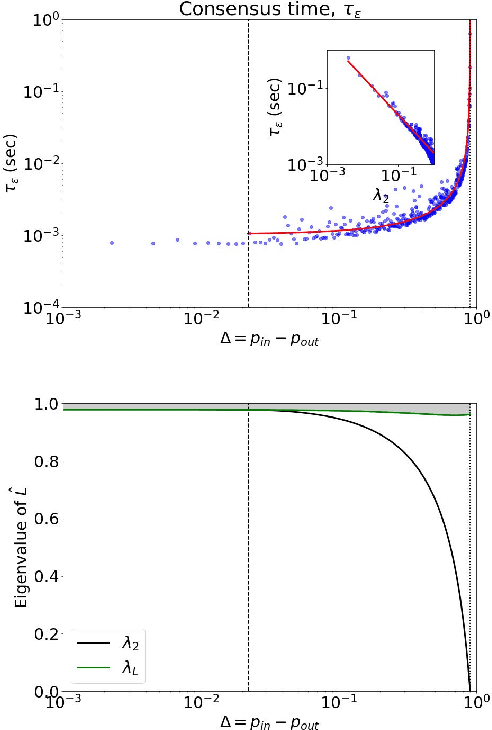
Consensus dynamics support decentralized machine learning for data that is distributed across a cloud compute cluster or across the internet of things. In these and other settings, one seeks to minimize the time $\tau_\epsilon$ required to obtain consensus within some $\epsilon>0$ margin of error. $\tau_\epsilon$ typically depends on the topology of the underlying communication network, and for many algorithms $\tau_\epsilon$ depends on the second-smallest eigenvalue $\lambda_2\in[0,1]$ of the network's normalized Laplacian matrix: $\tau_\epsilon\sim\mathcal{O}(\lambda_2^{-1})$. Here, we analyze the effect on $\tau_\epsilon$ of network community structure, which can arise when compute nodes/sensors are spatially clustered, for example. We study consensus machine learning over networks drawn from stochastic block models, which yield random networks that can contain heterogeneous communities with different sizes and densities. Using random matrix theory, we analyze the effects of communities on $\lambda_2$ and consensus, finding that $\lambda_2$ generally increases (i.e., $\tau_\epsilon$ decreases) as one decreases the extent of community structure. We further observe that there exists a critical level of community structure at which $\tau_\epsilon$ reaches a lower bound and is no longer limited by the presence of communities. We support our findings with empirical experiments for decentralized support vector machines.

Continuous-in-Depth Neural Networks

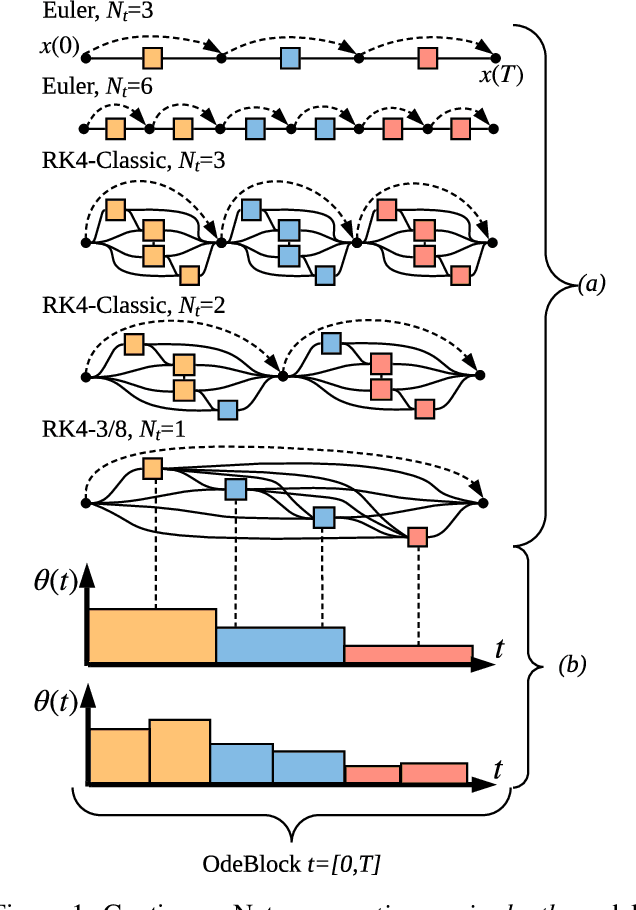
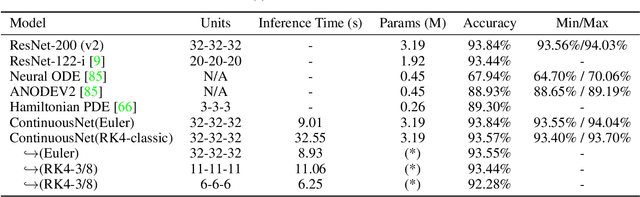
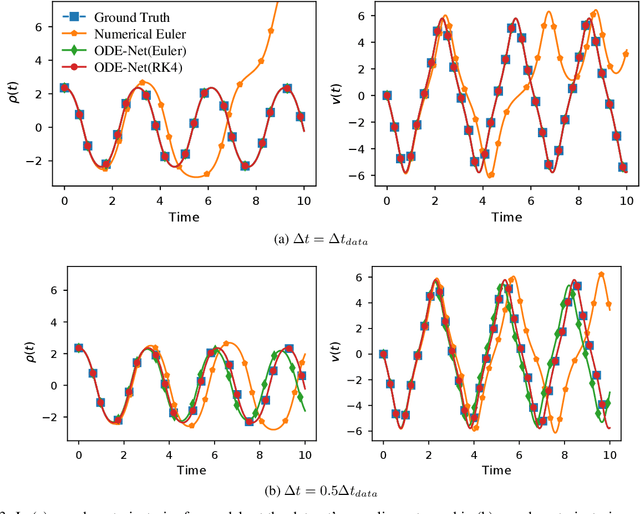
Recent work has attempted to interpret residual networks (ResNets) as one step of a forward Euler discretization of an ordinary differential equation, focusing mainly on syntactic algebraic similarities between the two systems. Discrete dynamical integrators of continuous dynamical systems, however, have a much richer structure. We first show that ResNets fail to be meaningful dynamical integrators in this richer sense. We then demonstrate that neural network models can learn to represent continuous dynamical systems, with this richer structure and properties, by embedding them into higher-order numerical integration schemes, such as the Runge Kutta schemes. Based on these insights, we introduce ContinuousNet as a continuous-in-depth generalization of ResNet architectures. ContinuousNets exhibit an invariance to the particular computational graph manifestation. That is, the continuous-in-depth model can be evaluated with different discrete time step sizes, which changes the number of layers, and different numerical integration schemes, which changes the graph connectivity. We show that this can be used to develop an incremental-in-depth training scheme that improves model quality, while significantly decreasing training time. We also show that, once trained, the number of units in the computational graph can even be decreased, for faster inference with little-to-no accuracy drop.

Noise-response Analysis for Rapid Detection of Backdoors in Deep Neural Networks

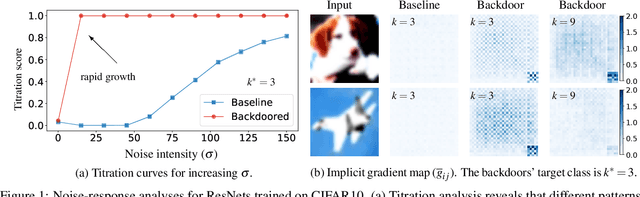
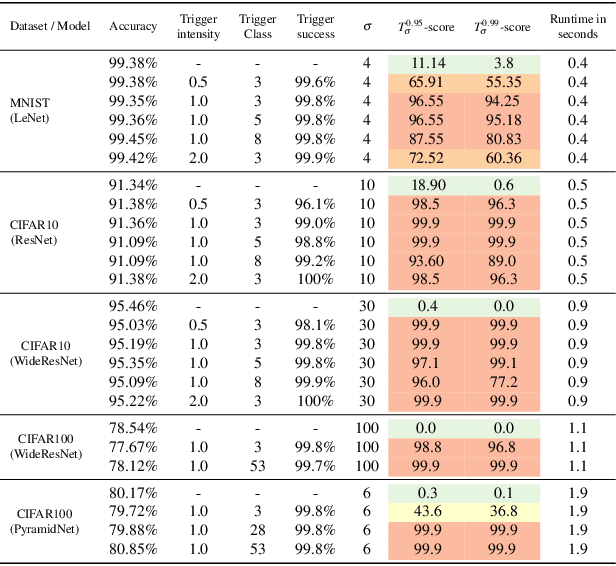
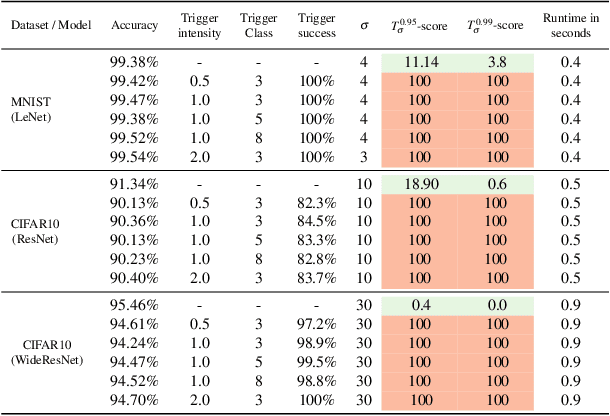
The pervasiveness of deep neural networks (DNNs) in technology, matched with the ubiquity of cloud-based training and transfer learning, is giving rise to a new frontier for cybersecurity whereby `structural malware' is manifest as compromised weights and activation pathways for unsecure DNNs. In particular, DNNs can be designed to have backdoors in which an adversary can easily and reliably fool a classifier by adding to any image a pattern of pixels called a trigger. Since DNNs are black-box algorithms, it is generally difficult to detect a backdoor or any other type of structural malware. To efficiently provide a reliable signal for the absence/presence of backdoors, we propose a rapid feature-generation step in which we study how DNNs respond to noise-infused images with varying noise intensity. This results in titration curves, which are a type of `fingerprinting' for DNNs. We find that DNNs with backdoors are more sensitive to input noise and respond in a characteristic way that reveals the backdoor and where it leads (i.e,. its target). Our empirical results demonstrate that we can accurately detect a backdoor with high confidence orders-of-magnitude faster than existing approaches (i.e., seconds versus hours). Our method also yields a titration-score that can automate the detection of compromised DNNs, whereas existing backdoor-detection strategies are not automated.

Clustering Network Layers With the Strata Multilayer Stochastic Block Model

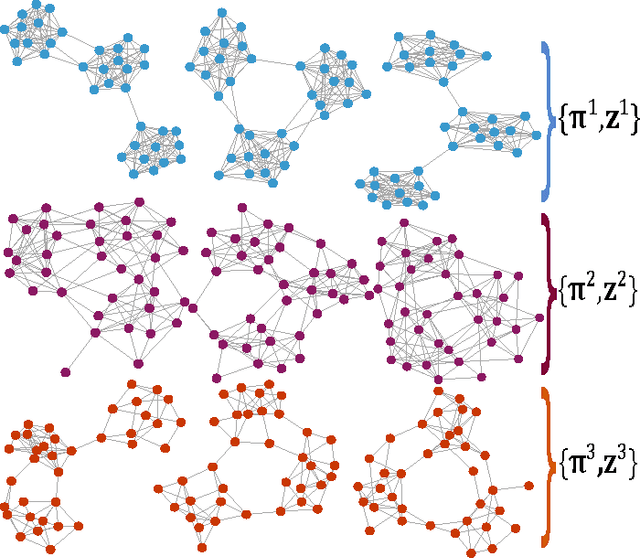
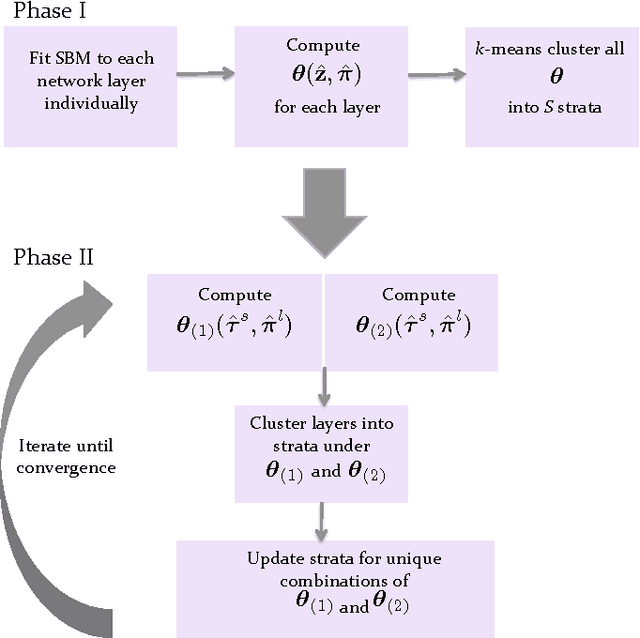
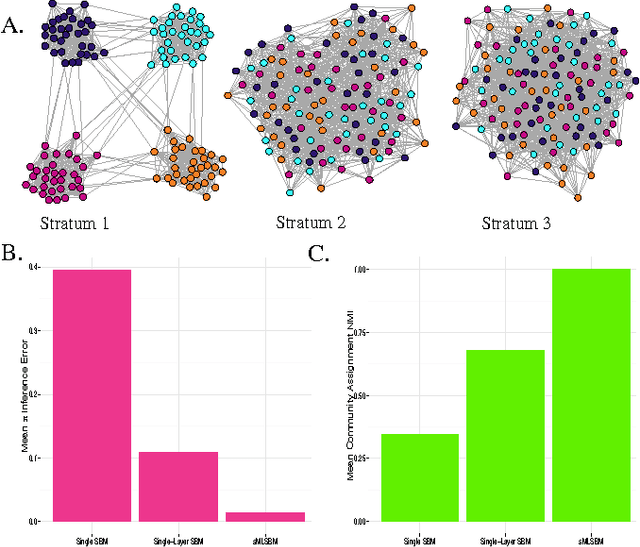
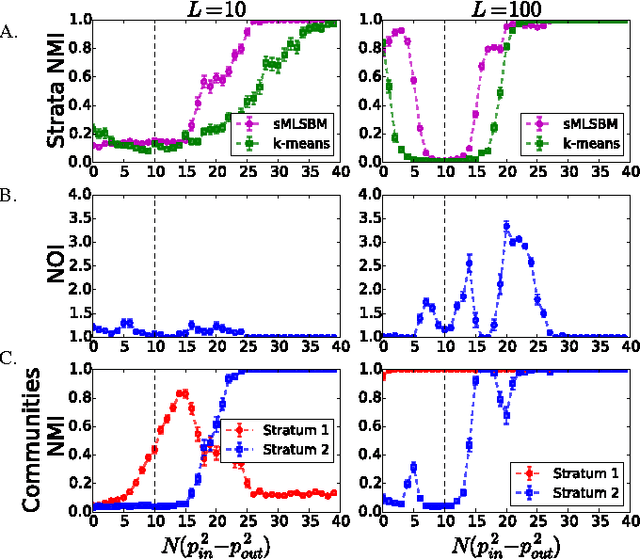
Multilayer networks are a useful data structure for simultaneously capturing multiple types of relationships between a set of nodes. In such networks, each relational definition gives rise to a layer. While each layer provides its own set of information, community structure across layers can be collectively utilized to discover and quantify underlying relational patterns between nodes. To concisely extract information from a multilayer network, we propose to identify and combine sets of layers with meaningful similarities in community structure. In this paper, we describe the "strata multilayer stochastic block model'' (sMLSBM), a probabilistic model for multilayer community structure. The central extension of the model is that there exist groups of layers, called "strata'', which are defined such that all layers in a given stratum have community structure described by a common stochastic block model (SBM). That is, layers in a stratum exhibit similar node-to-community assignments and SBM probability parameters. Fitting the sMLSBM to a multilayer network provides a joint clustering that yields node-to-community and layer-to-stratum assignments, which cooperatively aid one another during inference. We describe an algorithm for separating layers into their appropriate strata and an inference technique for estimating the SBM parameters for each stratum. We demonstrate our method using synthetic networks and a multilayer network inferred from data collected in the Human Microbiome Project.