HybridoNet-Adapt: A Domain-Adapted Framework for Accurate Lithium-Ion Battery RUL Prediction

Accurate prediction of the remaining useful life (RUL) in Lithium-ion battery (LIB) health management systems is crucial for ensuring reliability and safety. Current methods typically assume that training and testing data share the same distribution, overlooking the benefits of incorporating diverse data sources to enhance model performance. To address this limitation, we introduce a data-independent RUL prediction framework along with its domain adaptation (DA) approach, which leverages heterogeneous data sources for improved target predictions. Our approach integrates comprehensive data preprocessing, including feature extraction, denoising, and normalization, with a data-independent prediction model that combines Long Short-Term Memory (LSTM), Multihead Attention, and a Neural Ordinary Differential Equation (NODE) block, termed HybridoNet. The domain-adapted version, HybridoNet Adapt, is trained using a novel technique inspired by the Domain-Adversarial Neural Network (DANN) framework, a regression ensemble method, and Maximum Mean Discrepancy (MMD) to learn domain-invariant features from labeled cycling data in the source and target domains. Experimental results demonstrate that our approach outperforms state-of-the-art techniques, providing reliable RUL predictions for real-world applications.

Impact of Community Structure on Consensus Machine Learning

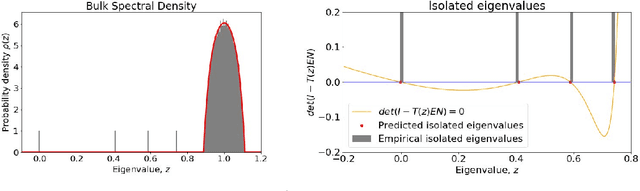
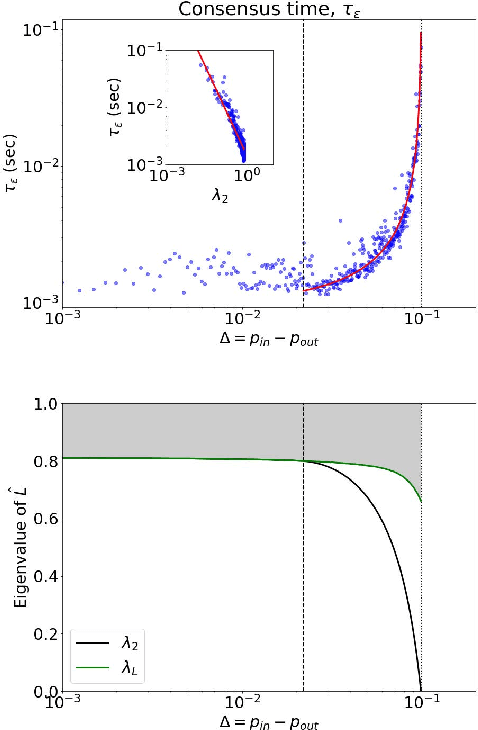
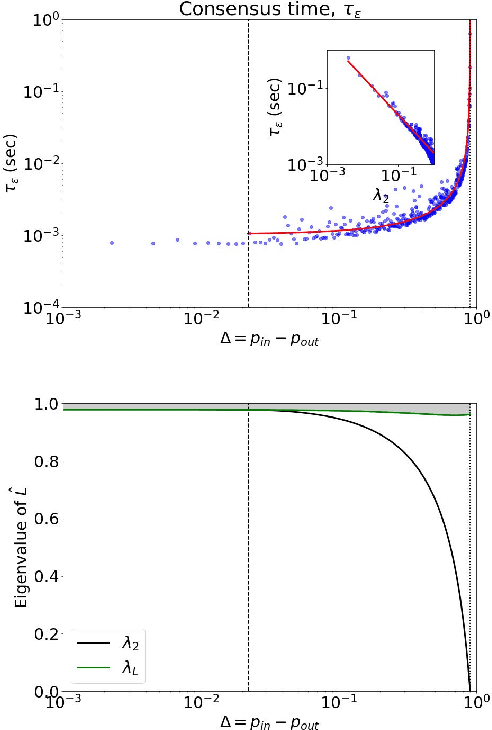
Consensus dynamics support decentralized machine learning for data that is distributed across a cloud compute cluster or across the internet of things. In these and other settings, one seeks to minimize the time $\tau_\epsilon$ required to obtain consensus within some $\epsilon>0$ margin of error. $\tau_\epsilon$ typically depends on the topology of the underlying communication network, and for many algorithms $\tau_\epsilon$ depends on the second-smallest eigenvalue $\lambda_2\in[0,1]$ of the network's normalized Laplacian matrix: $\tau_\epsilon\sim\mathcal{O}(\lambda_2^{-1})$. Here, we analyze the effect on $\tau_\epsilon$ of network community structure, which can arise when compute nodes/sensors are spatially clustered, for example. We study consensus machine learning over networks drawn from stochastic block models, which yield random networks that can contain heterogeneous communities with different sizes and densities. Using random matrix theory, we analyze the effects of communities on $\lambda_2$ and consensus, finding that $\lambda_2$ generally increases (i.e., $\tau_\epsilon$ decreases) as one decreases the extent of community structure. We further observe that there exists a critical level of community structure at which $\tau_\epsilon$ reaches a lower bound and is no longer limited by the presence of communities. We support our findings with empirical experiments for decentralized support vector machines.