Impact of Community Structure on Consensus Machine Learning
Paper and Code
Nov 02, 2020
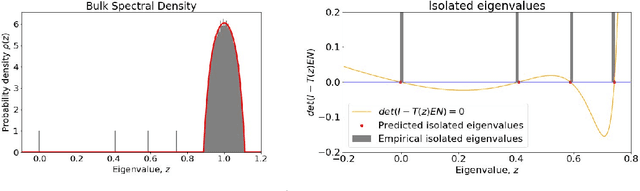
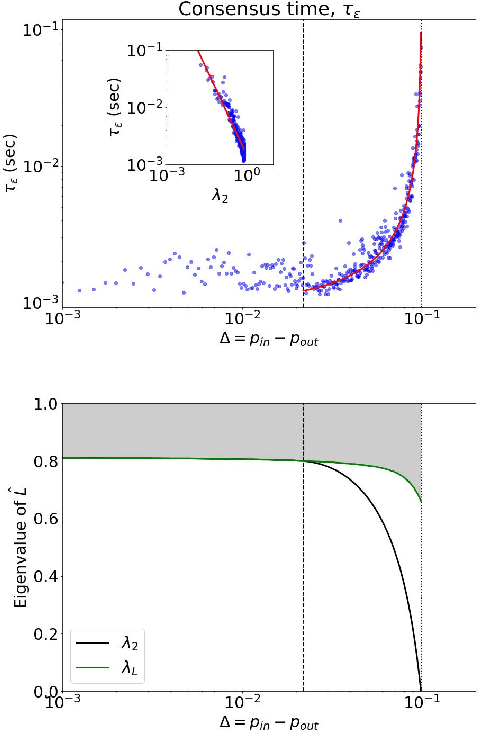
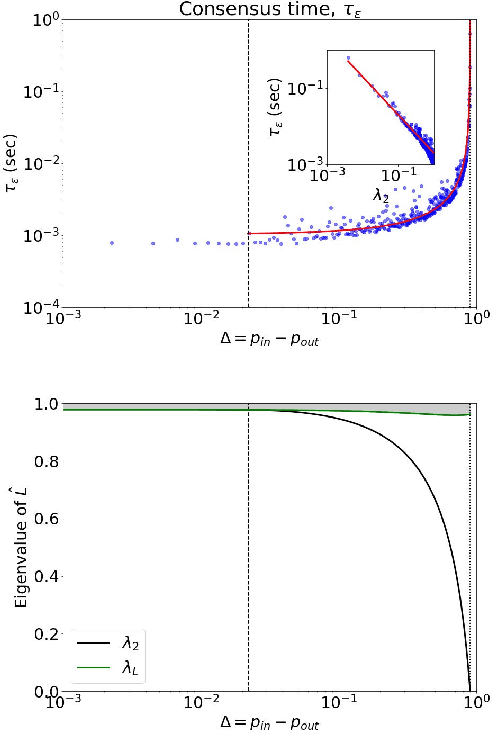
Consensus dynamics support decentralized machine learning for data that is distributed across a cloud compute cluster or across the internet of things. In these and other settings, one seeks to minimize the time $\tau_\epsilon$ required to obtain consensus within some $\epsilon>0$ margin of error. $\tau_\epsilon$ typically depends on the topology of the underlying communication network, and for many algorithms $\tau_\epsilon$ depends on the second-smallest eigenvalue $\lambda_2\in[0,1]$ of the network's normalized Laplacian matrix: $\tau_\epsilon\sim\mathcal{O}(\lambda_2^{-1})$. Here, we analyze the effect on $\tau_\epsilon$ of network community structure, which can arise when compute nodes/sensors are spatially clustered, for example. We study consensus machine learning over networks drawn from stochastic block models, which yield random networks that can contain heterogeneous communities with different sizes and densities. Using random matrix theory, we analyze the effects of communities on $\lambda_2$ and consensus, finding that $\lambda_2$ generally increases (i.e., $\tau_\epsilon$ decreases) as one decreases the extent of community structure. We further observe that there exists a critical level of community structure at which $\tau_\epsilon$ reaches a lower bound and is no longer limited by the presence of communities. We support our findings with empirical experiments for decentralized support vector machines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge