Conditional Similarity Triplets Enable Covariate-Informed Representations of Single-Cell Data

Single-cell technologies enable comprehensive profiling of diverse immune cell-types through the measurement of multiple genes or proteins per cell. In order to translate data from immune profiling assays into powerful diagnostics, machine learning approaches are used to compute per-sample immunological summaries, or featurizations that can be used as inputs to models for outcomes of interest. Current supervised learning approaches for computing per-sample representations are optimized based only on the outcome variable to be predicted and do not take into account clinically-relevant covariates that are likely to also be measured. Here we expand the optimization problem to also take into account such additional patient covariates to directly inform the learned per-sample representations. To do this, we introduce CytoCoSet, a set-based encoding method, which formulates a loss function with an additional triplet term penalizing samples with similar covariates from having disparate embedding results in per-sample representations. Overall, incorporating clinical covariates leads to improved prediction of clinical phenotypes.

Distribution-based Sketching of Single-Cell Samples

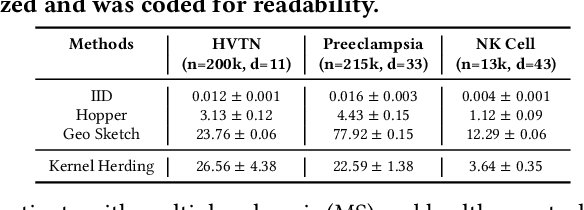
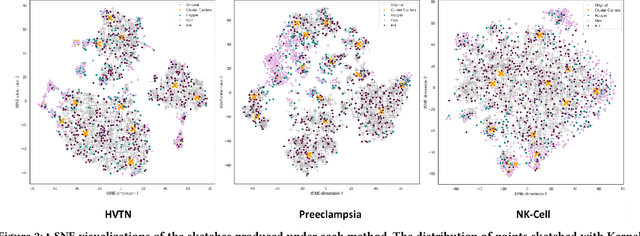
Modern high-throughput single-cell immune profiling technologies, such as flow and mass cytometry and single-cell RNA sequencing can readily measure the expression of a large number of protein or gene features across the millions of cells in a multi-patient cohort. While bioinformatics approaches can be used to link immune cell heterogeneity to external variables of interest, such as, clinical outcome or experimental label, they often struggle to accommodate such a large number of profiled cells. To ease this computational burden, a limited number of cells are typically \emph{sketched} or subsampled from each patient. However, existing sketching approaches fail to adequately subsample rare cells from rare cell-populations, or fail to preserve the true frequencies of particular immune cell-types. Here, we propose a novel sketching approach based on Kernel Herding that selects a limited subsample of all cells while preserving the underlying frequencies of immune cell-types. We tested our approach on three flow and mass cytometry datasets and on one single-cell RNA sequencing dataset and demonstrate that the sketched cells (1) more accurately represent the overall cellular landscape and (2) facilitate increased performance in downstream analysis tasks, such as classifying patients according to their clinical outcome. An implementation of sketching with Kernel Herding is publicly available at \url{https://github.com/vishalathreya/Set-Summarization}.

Interpretable Single-Cell Set Classification with Kernel Mean Embeddings

Modern single-cell flow and mass cytometry technologies measure the expression of several proteins of the individual cells within a blood or tissue sample. Each profiled biological sample is thus represented by a set of hundreds of thousands of multidimensional cell feature vectors, which incurs a high computational cost to predict each biological sample's associated phenotype with machine learning models. Such a large set cardinality also limits the interpretability of machine learning models due to the difficulty in tracking how each individual cell influences the ultimate prediction. Using Kernel Mean Embedding to encode the cellular landscape of each profiled biological sample, we can train a simple linear classifier and achieve state-of-the-art classification accuracy on 3 flow and mass cytometry datasets. Our model contains few parameters but still performs similarly to deep learning models with millions of parameters. In contrast with deep learning approaches, the linearity and sub-selection step of our model make it easy to interpret classification results. Clustering analysis further shows that our method admits rich biological interpretability for linking cellular heterogeneity to clinical phenotype.

Stochastic Block Models with Multiple Continuous Attributes

The stochastic block model (SBM) is a probabilistic model for community structure in networks. Typically, only the adjacency matrix is used to perform SBM parameter inference. In this paper, we consider circumstances in which nodes have an associated vector of continuous attributes that are also used to learn the node-to-community assignments and corresponding SBM parameters. While this assumption is not realistic for every application, our model assumes that the attributes associated with the nodes in a network's community can be described by a common multivariate Gaussian model. In this augmented, attributed SBM, the objective is to simultaneously learn the SBM connectivity probabilities with the multivariate Gaussian parameters describing each community. While there are recent examples in the literature that combine connectivity and attribute information to inform community detection, our model is the first augmented stochastic block model to handle multiple continuous attributes. This provides the flexibility in biological data to, for example, augment connectivity information with continuous measurements from multiple experimental modalities. Because the lack of labeled network data often makes community detection results difficult to validate, we highlight the usefulness of our model for two network prediction tasks: link prediction and collaborative filtering. As a result of fitting this attributed stochastic block model, one can predict the attribute vector or connectivity patterns for a new node in the event of the complementary source of information (connectivity or attributes, respectively). We also highlight two biological examples where the attributed stochastic block model provides satisfactory performance in the link prediction and collaborative filtering tasks.

Clustering Network Layers With the Strata Multilayer Stochastic Block Model

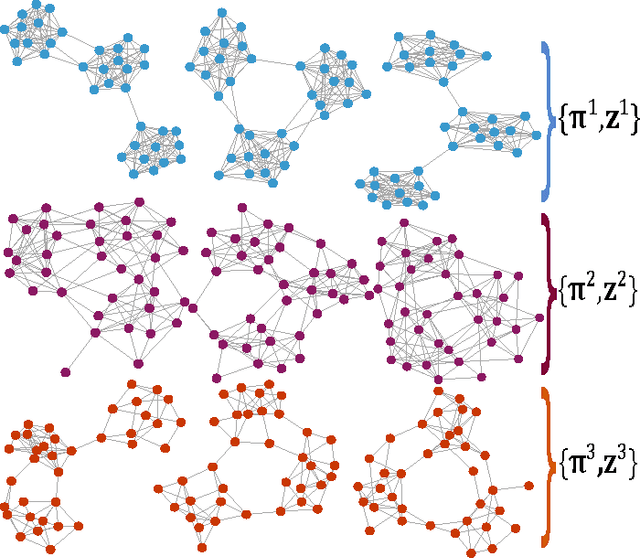
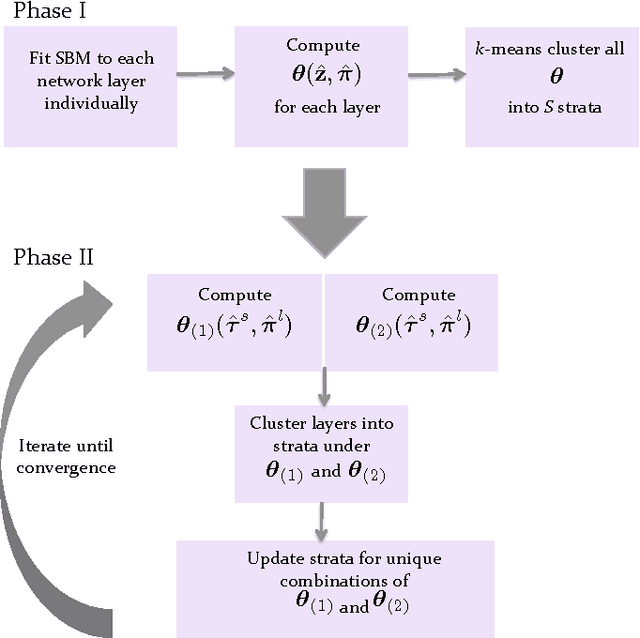
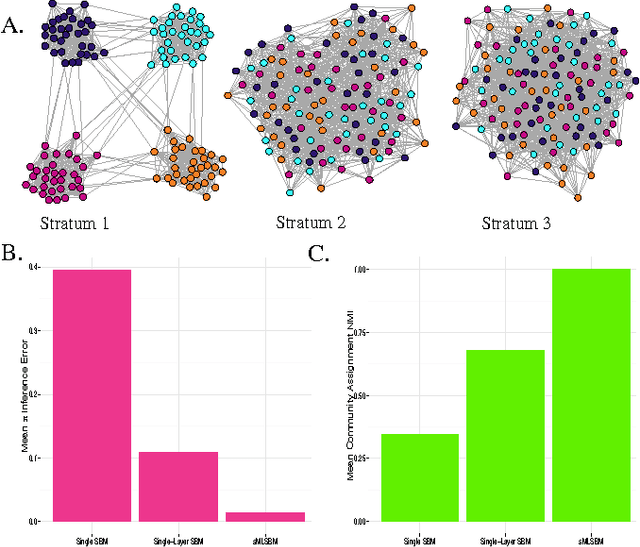
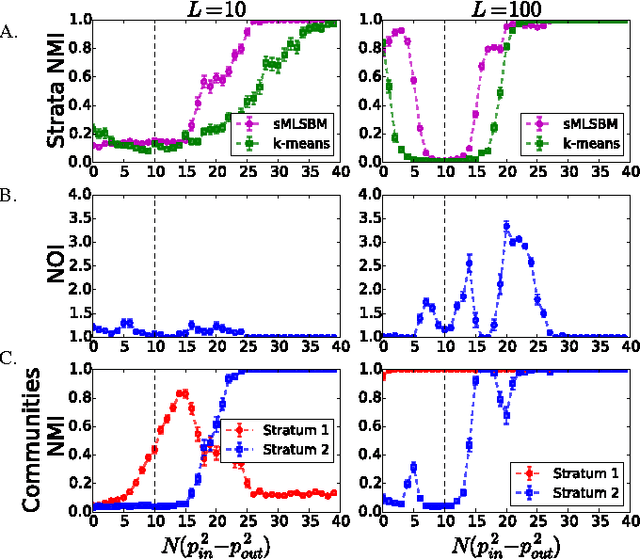
Multilayer networks are a useful data structure for simultaneously capturing multiple types of relationships between a set of nodes. In such networks, each relational definition gives rise to a layer. While each layer provides its own set of information, community structure across layers can be collectively utilized to discover and quantify underlying relational patterns between nodes. To concisely extract information from a multilayer network, we propose to identify and combine sets of layers with meaningful similarities in community structure. In this paper, we describe the "strata multilayer stochastic block model'' (sMLSBM), a probabilistic model for multilayer community structure. The central extension of the model is that there exist groups of layers, called "strata'', which are defined such that all layers in a given stratum have community structure described by a common stochastic block model (SBM). That is, layers in a stratum exhibit similar node-to-community assignments and SBM probability parameters. Fitting the sMLSBM to a multilayer network provides a joint clustering that yields node-to-community and layer-to-stratum assignments, which cooperatively aid one another during inference. We describe an algorithm for separating layers into their appropriate strata and an inference technique for estimating the SBM parameters for each stratum. We demonstrate our method using synthetic networks and a multilayer network inferred from data collected in the Human Microbiome Project.