Learning continuous models for continuous physics

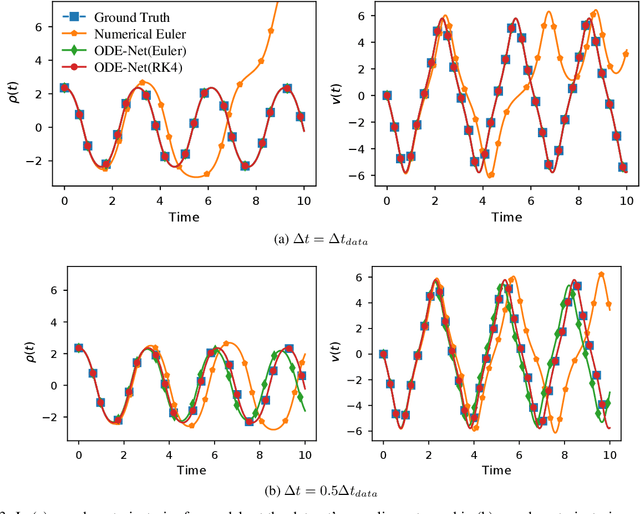
Dynamical systems that evolve continuously over time are ubiquitous throughout science and engineering. Machine learning (ML) provides data-driven approaches to model and predict the dynamics of such systems. A core issue with this approach is that ML models are typically trained on discrete data, using ML methodologies that are not aware of underlying continuity properties, which results in models that often do not capture the underlying continuous dynamics of a system of interest. As a result, these ML models are of limited use for for many scientific and engineering applications. To address this challenge, we develop a convergence test based on numerical analysis theory. Our test verifies whether a model has learned a function that accurately approximates a system's underlying continuous dynamics. Models that fail this test fail to capture relevant dynamics, rendering them of limited utility for many scientific prediction tasks; while models that pass this test enable both better interpolation and better extrapolation in multiple ways. Our results illustrate how principled numerical analysis methods can be coupled with existing ML training/testing methodologies to validate models for science and engineering applications.

Continuous-in-Depth Neural Networks

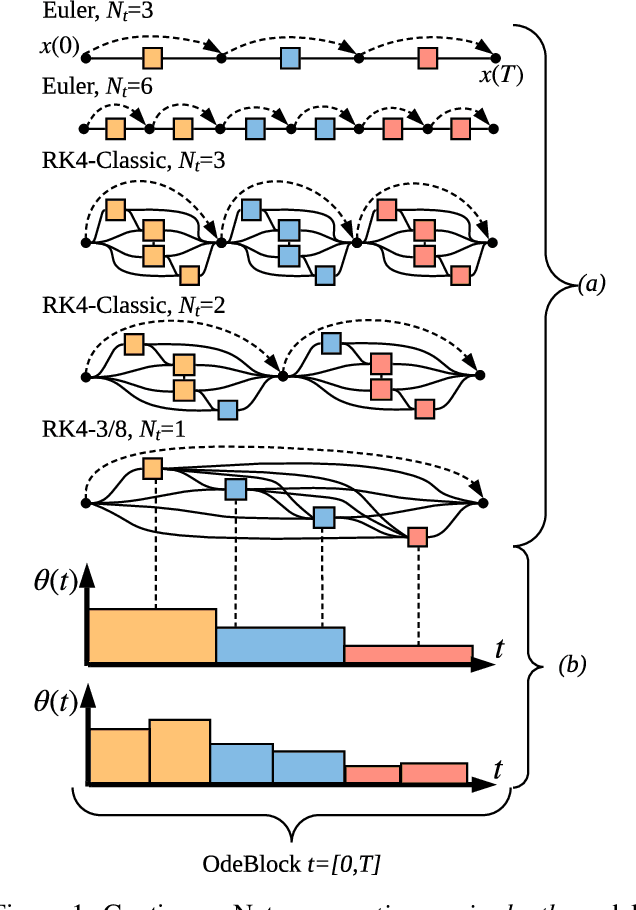
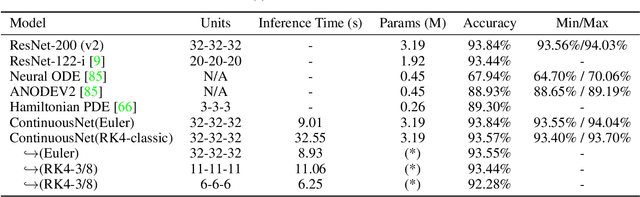
Recent work has attempted to interpret residual networks (ResNets) as one step of a forward Euler discretization of an ordinary differential equation, focusing mainly on syntactic algebraic similarities between the two systems. Discrete dynamical integrators of continuous dynamical systems, however, have a much richer structure. We first show that ResNets fail to be meaningful dynamical integrators in this richer sense. We then demonstrate that neural network models can learn to represent continuous dynamical systems, with this richer structure and properties, by embedding them into higher-order numerical integration schemes, such as the Runge Kutta schemes. Based on these insights, we introduce ContinuousNet as a continuous-in-depth generalization of ResNet architectures. ContinuousNets exhibit an invariance to the particular computational graph manifestation. That is, the continuous-in-depth model can be evaluated with different discrete time step sizes, which changes the number of layers, and different numerical integration schemes, which changes the graph connectivity. We show that this can be used to develop an incremental-in-depth training scheme that improves model quality, while significantly decreasing training time. We also show that, once trained, the number of units in the computational graph can even be decreased, for faster inference with little-to-no accuracy drop.