A dynamical systems based framework for dimension reduction

We propose a novel framework for learning a low-dimensional representation of data based on nonlinear dynamical systems, which we call dynamical dimension reduction (DDR). In the DDR model, each point is evolved via a nonlinear flow towards a lower-dimensional subspace; the projection onto the subspace gives the low-dimensional embedding. Training the model involves identifying the nonlinear flow and the subspace. Following the equation discovery method, we represent the vector field that defines the flow using a linear combination of dictionary elements, where each element is a pre-specified linear/nonlinear candidate function. A regularization term for the average total kinetic energy is also introduced and motivated by optimal transport theory. We prove that the resulting optimization problem is well-posed and establish several properties of the DDR method. We also show how the DDR method can be trained using a gradient-based optimization method, where the gradients are computed using the adjoint method from optimal control theory. The DDR method is implemented and compared on synthetic and example datasets to other dimension reductions methods, including PCA, t-SNE, and Umap.

A non-autonomous equation discovery method for time signal classification

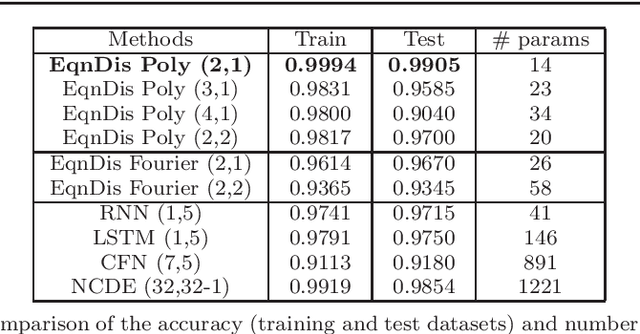
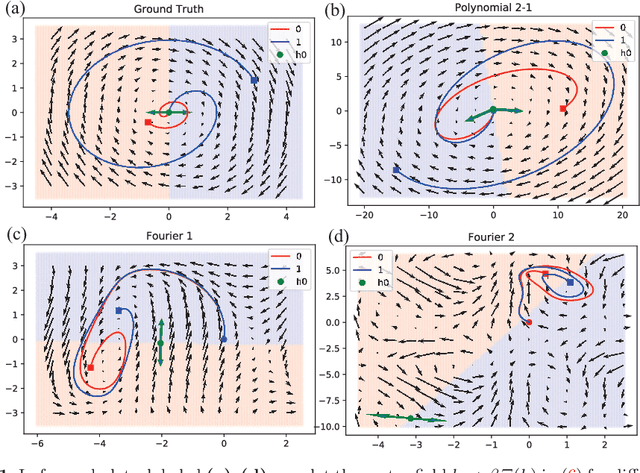
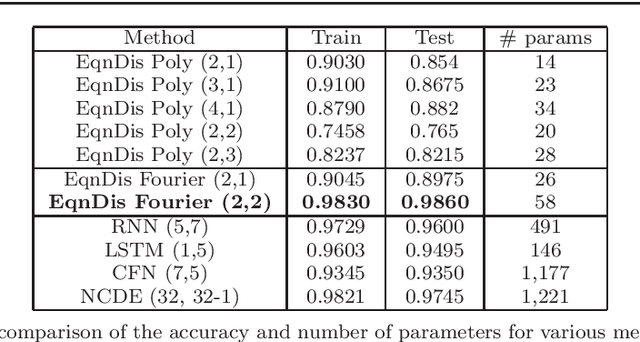
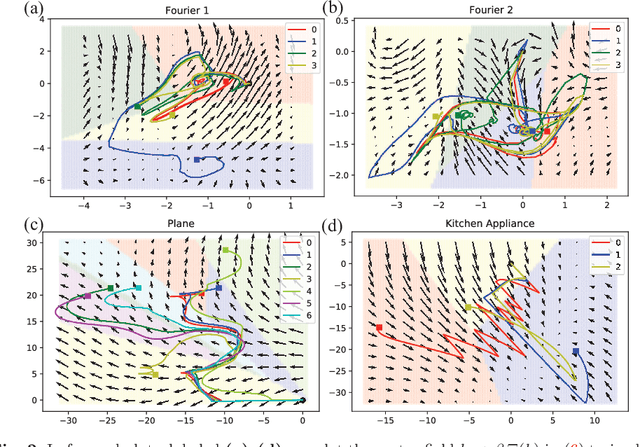
Certain neural network architectures, in the infinite-layer limit, lead to systems of nonlinear differential equations. Motivated by this idea, we develop a framework for analyzing time signals based on non-autonomous dynamical equations. We view the time signal as a forcing function for a dynamical system that governs a time-evolving hidden variable. As in equation discovery, the dynamical system is represented using a dictionary of functions and the coefficients are learned from data. This framework is applied to the time signal classification problem. We show how gradients can be efficiently computed using the adjoint method, and we apply methods from dynamical systems to establish stability of the classifier. Through a variety of experiments, on both synthetic and real datasets, we show that the proposed method uses orders of magnitude fewer parameters than competing methods, while achieving comparable accuracy. We created the synthetic datasets using dynamical systems of increasing complexity; though the ground truth vector fields are often polynomials, we find consistently that a Fourier dictionary yields the best results. We also demonstrate how the proposed method yields graphical interpretability in the form of phase portraits.