A Survey on Large Language Model-based Agents for Statistics and Data Science

In recent years, data science agents powered by Large Language Models (LLMs), known as "data agents," have shown significant potential to transform the traditional data analysis paradigm. This survey provides an overview of the evolution, capabilities, and applications of LLM-based data agents, highlighting their role in simplifying complex data tasks and lowering the entry barrier for users without related expertise. We explore current trends in the design of LLM-based frameworks, detailing essential features such as planning, reasoning, reflection, multi-agent collaboration, user interface, knowledge integration, and system design, which enable agents to address data-centric problems with minimal human intervention. Furthermore, we analyze several case studies to demonstrate the practical applications of various data agents in real-world scenarios. Finally, we identify key challenges and propose future research directions to advance the development of data agents into intelligent statistical analysis software.

LAMBDA: A Large Model Based Data Agent

We introduce ``LAMBDA," a novel open-source, code-free multi-agent data analysis system that that harnesses the power of large models. LAMBDA is designed to address data analysis challenges in complex data-driven applications through the use of innovatively designed data agents that operate iteratively and generatively using natural language. At the core of LAMBDA are two key agent roles: the programmer and the inspector, which are engineered to work together seamlessly. Specifically, the programmer generates code based on the user's instructions and domain-specific knowledge, enhanced by advanced models. Meanwhile, the inspector debugs the code when necessary. To ensure robustness and handle adverse scenarios, LAMBDA features a user interface that allows direct user intervention in the operational loop. Additionally, LAMBDA can flexibly integrate external models and algorithms through our knowledge integration mechanism, catering to the needs of customized data analysis. LAMBDA has demonstrated strong performance on various machine learning datasets. It has the potential to enhance data science practice and analysis paradigm by seamlessly integrating human and artificial intelligence, making it more accessible, effective, and efficient for individuals from diverse backgrounds. The strong performance of LAMBDA in solving data science problems is demonstrated in several case studies, which are presented at \url{https://www.polyu.edu.hk/ama/cmfai/lambda.html}.

Statistical ranking with dynamic covariates

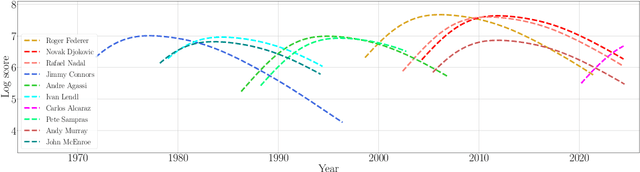
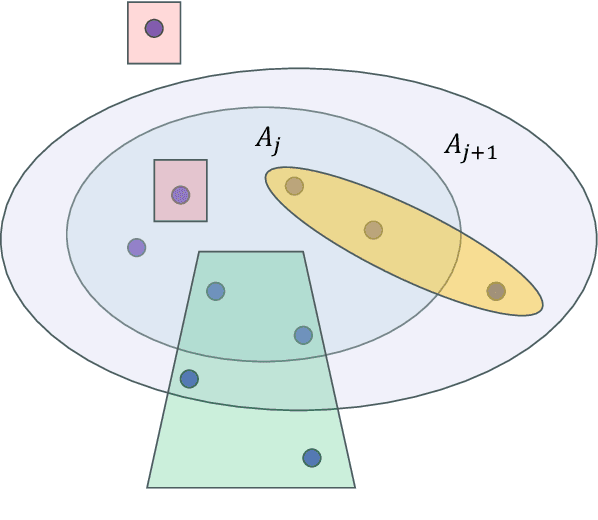
We consider a covariate-assisted ranking model grounded in the Plackett--Luce framework. Unlike existing works focusing on pure covariates or individual effects with fixed covariates, our approach integrates individual effects with dynamic covariates. This added flexibility enhances realistic ranking yet poses significant challenges for analyzing the associated estimation procedures. This paper makes an initial attempt to address these challenges. We begin by discussing the sufficient and necessary condition for the model's identifiability. We then introduce an efficient alternating maximization algorithm to compute the maximum likelihood estimator (MLE). Under suitable assumptions on the topology of comparison graphs and dynamic covariates, we establish a quantitative uniform consistency result for the MLE with convergence rates characterized by the asymptotic graph connectivity. The proposed graph topology assumption holds for several popular random graph models under optimal leading-order sparsity conditions. A comprehensive numerical study is conducted to corroborate our theoretical findings and demonstrate the application of the proposed model to real-world datasets, including horse racing and tennis competitions.

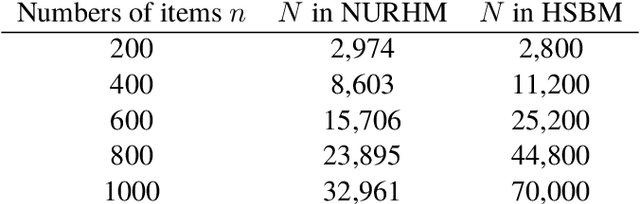
Adaptive debiased SGD in high-dimensional GLMs with steaming data

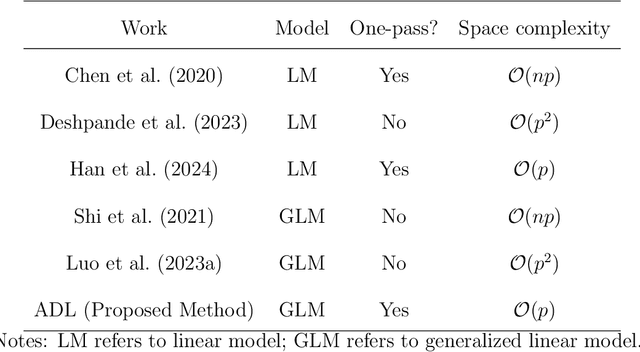
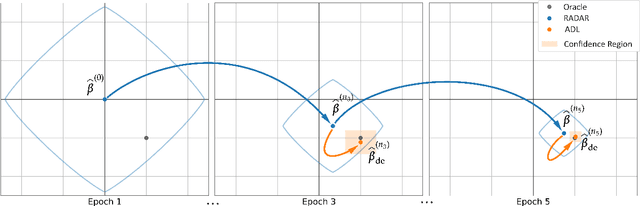
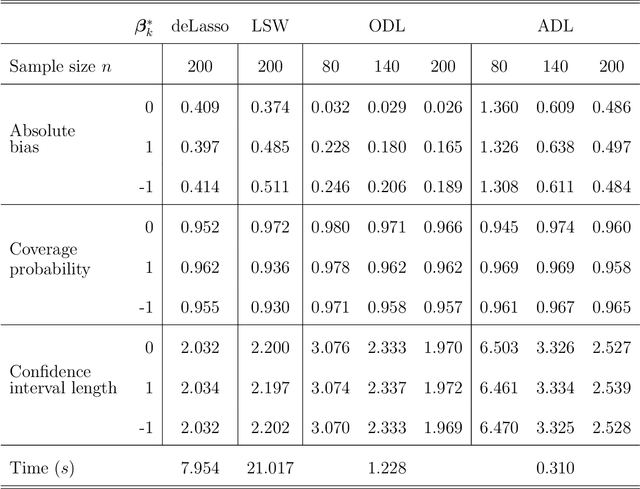
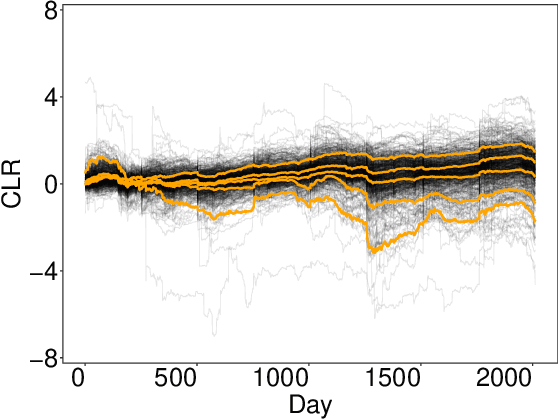
Online statistical inference facilitates real-time analysis of sequentially collected data, making it different from traditional methods that rely on static datasets. This paper introduces a novel approach to online inference in high-dimensional generalized linear models, where we update regression coefficient estimates and their standard errors upon each new data arrival. In contrast to existing methods that either require full dataset access or large-dimensional summary statistics storage, our method operates in a single-pass mode, significantly reducing both time and space complexity. The core of our methodological innovation lies in an adaptive stochastic gradient descent algorithm tailored for dynamic objective functions, coupled with a novel online debiasing procedure. This allows us to maintain low-dimensional summary statistics while effectively controlling optimization errors introduced by the dynamically changing loss functions. We demonstrate that our method, termed the Approximated Debiased Lasso (ADL), not only mitigates the need for the bounded individual probability condition but also significantly improves numerical performance. Numerical experiments demonstrate that the proposed ADL method consistently exhibits robust performance across various covariance matrix structures.

Statistical inference for pairwise comparison models

Pairwise comparison models are used for quantitatively evaluating utility and ranking in various fields. The increasing scale of modern problems underscores the need to understand statistical inference in these models when the number of subjects diverges, which is currently lacking in the literature except in a few special instances. This paper addresses this gap by establishing an asymptotic normality result for the maximum likelihood estimator in a broad class of pairwise comparison models. The key idea lies in identifying the Fisher information matrix as a weighted graph Laplacian matrix which can be studied via a meticulous spectral analysis. Our findings provide the first unified theory for performing statistical inference in a wide range of pairwise comparison models beyond the Bradley--Terry model, benefiting practitioners with a solid theoretical guarantee for their use. Simulations utilizing synthetic data are conducted to validate the asymptotic normality result, followed by a hypothesis test using a tennis competition dataset.

Probabilistic methods for approximate archetypal analysis

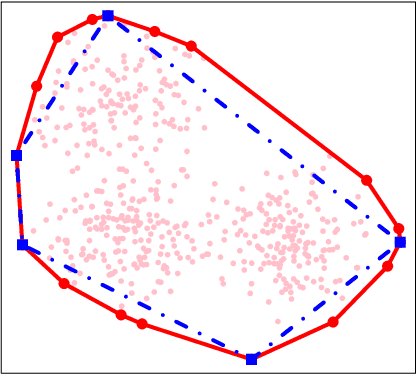
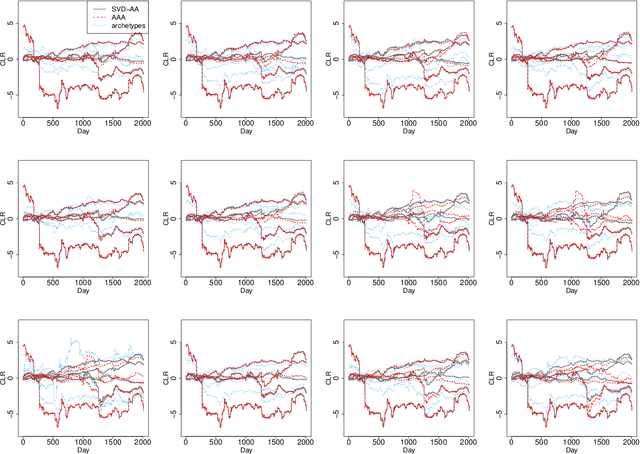
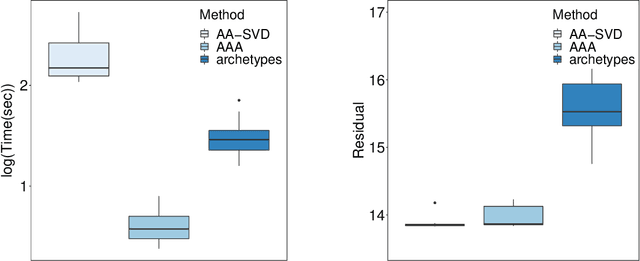
Archetypal analysis is an unsupervised learning method for exploratory data analysis. One major challenge that limits the applicability of archetypal analysis in practice is the inherent computational complexity of the existing algorithms. In this paper, we provide a novel approximation approach to partially address this issue. Utilizing probabilistic ideas from high-dimensional geometry, we introduce two preprocessing techniques to reduce the dimension and representation cardinality of the data, respectively. We prove that, provided the data is approximately embedded in a low-dimensional linear subspace and the convex hull of the corresponding representations is well approximated by a polytope with a few vertices, our method can effectively reduce the scaling of archetypal analysis. Moreover, the solution of the reduced problem is near-optimal in terms of prediction errors. Our approach can be combined with other acceleration techniques to further mitigate the intrinsic complexity of archetypal analysis. We demonstrate the usefulness of our results by applying our method to summarize several moderately large-scale datasets.

A General Pairwise Comparison Model for Extremely Sparse Networks

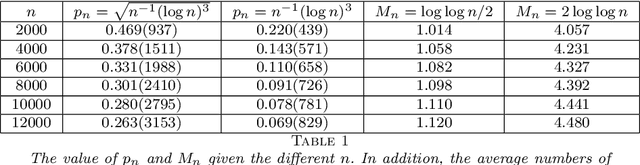
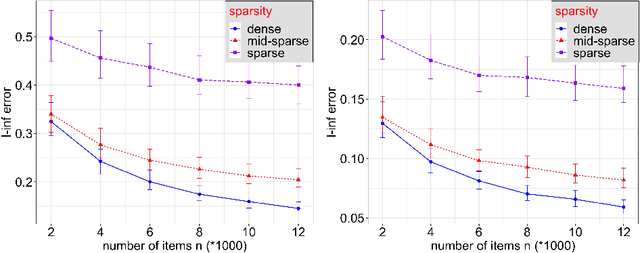
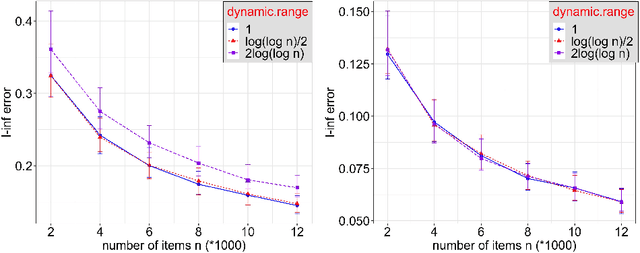
Statistical inference using pairwise comparison data has been an effective approach to analyzing complex and sparse networks. In this paper we propose a general framework for modeling the mutual interaction in a probabilistic network, which enjoys ample flexibility in terms of parametrization. Within this set-up, we establish that the maximum likelihood estimator (MLE) for the latent scores of the subjects is uniformly consistent under a near-minimal condition on network sparsity. This condition is sharp in terms of the leading order asymptotics describing the sparsity. The proof utilizes a novel chaining technique based on the error-induced metric as well as careful counting of comparison graph structures. Our results guarantee that the MLE is a valid estimator for inference in large-scale comparison networks where data is asymptotically deficient. Numerical simulations are provided to complement the theoretical analysis.

Curiosity-Driven Recommendation Strategy for Adaptive Learning via Deep Reinforcement Learning

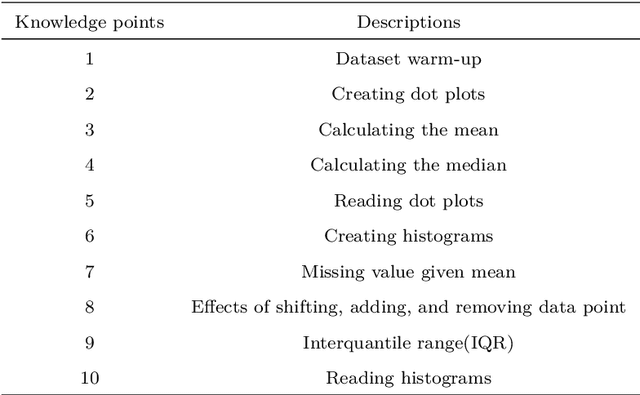
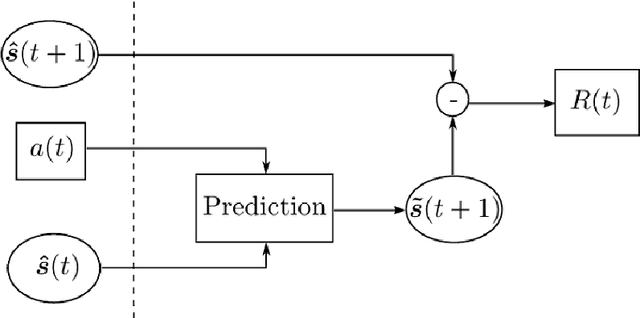
The design of recommendations strategies in the adaptive learning system focuses on utilizing currently available information to provide individual-specific learning instructions for learners. As a critical motivate for human behaviors, curiosity is essentially the drive to explore knowledge and seek information. In a psychologically inspired view, we aim to incorporate the element of curiosity for guiding learners to study spontaneously. In this paper, a curiosity-driven recommendation policy is proposed under the reinforcement learning framework, allowing for a both efficient and enjoyable personalized learning mode. Given intrinsic rewards from a well-designed predictive model, we apply the actor-critic method to approximate the policy directly through neural networks. Numeric analyses with a large continuous knowledge state space and concrete learning scenarios are used to further demonstrate the power of the proposed method.