Conformal Set-based Human-AI Complementarity with Multiple Experts

Decision support systems are designed to assist human experts in classification tasks by providing conformal prediction sets derived from a pre-trained model. This human-AI collaboration has demonstrated enhanced classification performance compared to using either the model or the expert independently. In this study, we focus on the selection of instance-specific experts from a pool of multiple human experts, contrasting it with existing research that typically focuses on single-expert scenarios. We characterize the conditions under which multiple experts can benefit from the conformal sets. With the insight that only certain experts may be relevant for each instance, we explore the problem of subset selection and introduce a greedy algorithm that utilizes conformal sets to identify the subset of expert predictions that will be used in classifying an instance. This approach is shown to yield better performance compared to naive methods for human subset selection. Based on real expert predictions from the CIFAR-10H and ImageNet-16H datasets, our simulation study indicates that our proposed greedy algorithm achieves near-optimal subsets, resulting in improved classification performance among multiple experts.

Learning Guarantee of Reward Modeling Using Deep Neural Networks

In this work, we study the learning theory of reward modeling with pairwise comparison data using deep neural networks. We establish a novel non-asymptotic regret bound for deep reward estimators in a non-parametric setting, which depends explicitly on the network architecture. Furthermore, to underscore the critical importance of clear human beliefs, we introduce a margin-type condition that assumes the conditional winning probability of the optimal action in pairwise comparisons is significantly distanced from 1/2. This condition enables a sharper regret bound, which substantiates the empirical efficiency of Reinforcement Learning from Human Feedback and highlights clear human beliefs in its success. Notably, this improvement stems from high-quality pairwise comparison data implied by the margin-type condition, is independent of the specific estimators used, and thus applies to various learning algorithms and models.

Deep Distributional Learning with Non-crossing Quantile Network

In this paper, we introduce a non-crossing quantile (NQ) network for conditional distribution learning. By leveraging non-negative activation functions, the NQ network ensures that the learned distributions remain monotonic, effectively addressing the issue of quantile crossing. Furthermore, the NQ network-based deep distributional learning framework is highly adaptable, applicable to a wide range of applications, from classical non-parametric quantile regression to more advanced tasks such as causal effect estimation and distributional reinforcement learning (RL). We also develop a comprehensive theoretical foundation for the deep NQ estimator and its application to distributional RL, providing an in-depth analysis that demonstrates its effectiveness across these domains. Our experimental results further highlight the robustness and versatility of the NQ network.

Conditional Stochastic Interpolation for Generative Learning

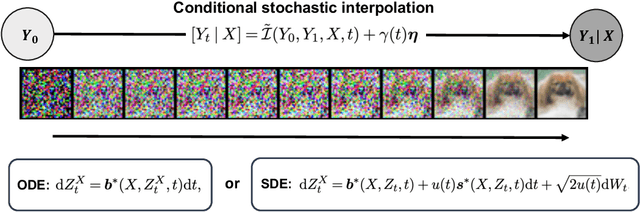
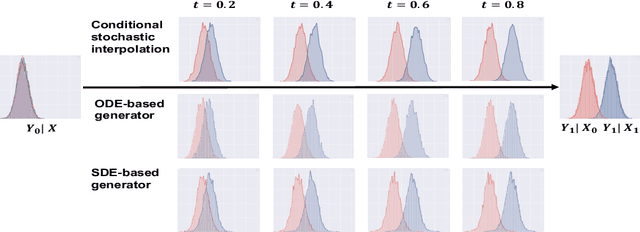
We propose a conditional stochastic interpolation (CSI) approach to learning conditional distributions. CSI learns probability flow equations or stochastic differential equations that transport a reference distribution to the target conditional distribution. This is achieved by first learning the drift function and the conditional score function based on conditional stochastic interpolation, which are then used to construct a deterministic process governed by an ordinary differential equation or a diffusion process for conditional sampling. In our proposed CSI model, we incorporate an adaptive diffusion term to address the instability issues arising during the training process. We provide explicit forms of the conditional score function and the drift function in terms of conditional expectations under mild conditions, which naturally lead to an nonparametric regression approach to estimating these functions. Furthermore, we establish non-asymptotic error bounds for learning the target conditional distribution via conditional stochastic interpolation in terms of KL divergence, taking into account the neural network approximation error. We illustrate the application of CSI on image generation using a benchmark image dataset.

Wasserstein Generative Regression

In this paper, we propose a new and unified approach for nonparametric regression and conditional distribution learning. Our approach simultaneously estimates a regression function and a conditional generator using a generative learning framework, where a conditional generator is a function that can generate samples from a conditional distribution. The main idea is to estimate a conditional generator that satisfies the constraint that it produces a good regression function estimator. We use deep neural networks to model the conditional generator. Our approach can handle problems with multivariate outcomes and covariates, and can be used to construct prediction intervals. We provide theoretical guarantees by deriving non-asymptotic error bounds and the distributional consistency of our approach under suitable assumptions. We also perform numerical experiments with simulated and real data to demonstrate the effectiveness and superiority of our approach over some existing approaches in various scenarios.

Complexity of Feed-Forward Neural Networks from the Perspective of Functional Equivalence

In this paper, we investigate the complexity of feed-forward neural networks by examining the concept of functional equivalence, which suggests that different network parameterizations can lead to the same function. We utilize the permutation invariance property to derive a novel covering number bound for the class of feedforward neural networks, which reveals that the complexity of a neural network can be reduced by exploiting this property. Furthermore, based on the symmetric structure of parameter space, we demonstrate that an appropriate strategy of random parameter initialization can increase the probability of convergence for optimization. We found that overparameterized networks tend to be easier to train in the sense that increasing the width of neural networks leads to a vanishing volume of the effective parameter space. Our findings offer new insights into overparameterization and have significant implications for understanding generalization and optimization in deep learning.

Differentiable Neural Networks with RePU Activation: with Applications to Score Estimation and Isotonic Regression

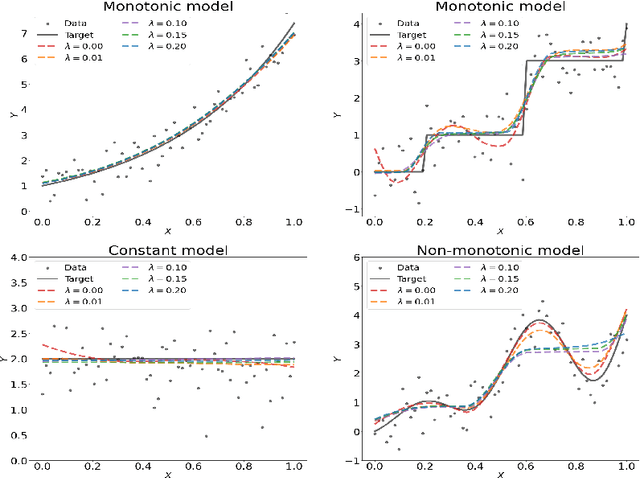
We study the properties of differentiable neural networks activated by rectified power unit (RePU) functions. We show that the partial derivatives of RePU neural networks can be represented by RePUs mixed-activated networks and derive upper bounds for the complexity of the function class of derivatives of RePUs networks. We establish error bounds for simultaneously approximating $C^s$ smooth functions and their derivatives using RePU-activated deep neural networks. Furthermore, we derive improved approximation error bounds when data has an approximate low-dimensional support, demonstrating the ability of RePU networks to mitigate the curse of dimensionality. To illustrate the usefulness of our results, we consider a deep score matching estimator (DSME) and propose a penalized deep isotonic regression (PDIR) using RePU networks. We establish non-asymptotic excess risk bounds for DSME and PDIR under the assumption that the target functions belong to a class of $C^s$ smooth functions. We also show that PDIR has a robustness property in the sense it is consistent with vanishing penalty parameters even when the monotonicity assumption is not satisfied. Furthermore, if the data distribution is supported on an approximate low-dimensional manifold, we show that DSME and PDIR can mitigate the curse of dimensionality.

Nonparametric Quantile Regression: Non-Crossing Constraints and Conformal Prediction

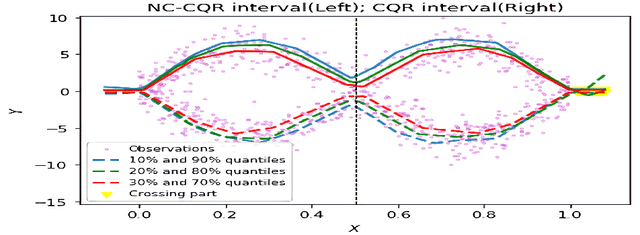
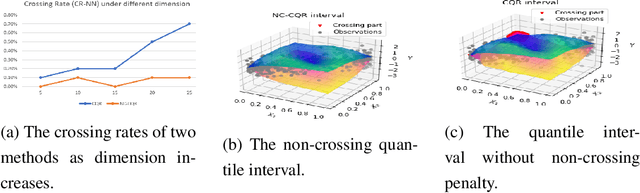
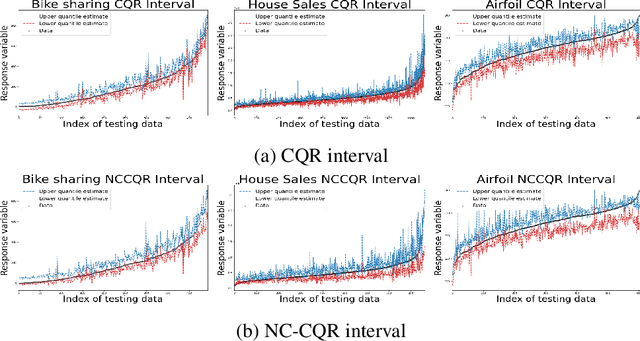
We propose a nonparametric quantile regression method using deep neural networks with a rectified linear unit penalty function to avoid quantile crossing. This penalty function is computationally feasible for enforcing non-crossing constraints in multi-dimensional nonparametric quantile regression. We establish non-asymptotic upper bounds for the excess risk of the proposed nonparametric quantile regression function estimators. Our error bounds achieve optimal minimax rate of convergence for the Holder class, and the prefactors of the error bounds depend polynomially on the dimension of the predictor, instead of exponentially. Based on the proposed non-crossing penalized deep quantile regression, we construct conformal prediction intervals that are fully adaptive to heterogeneity. The proposed prediction interval is shown to have good properties in terms of validity and accuracy under reasonable conditions. We also derive non-asymptotic upper bounds for the difference of the lengths between the proposed non-crossing conformal prediction interval and the theoretically oracle prediction interval. Numerical experiments including simulation studies and a real data example are conducted to demonstrate the effectiveness of the proposed method.

Estimation of Non-Crossing Quantile Regression Process with Deep ReQU Neural Networks

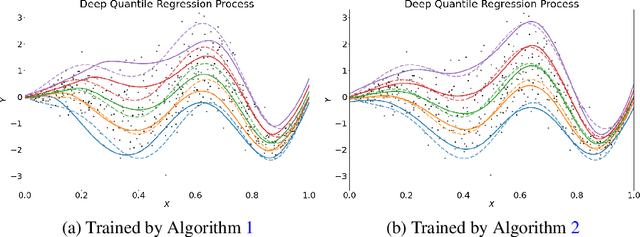
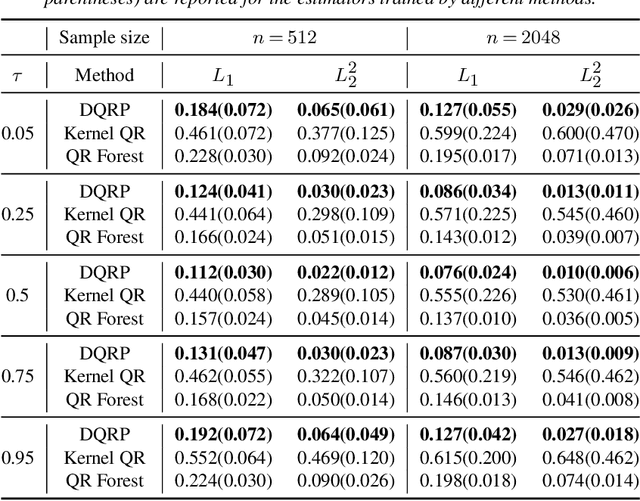
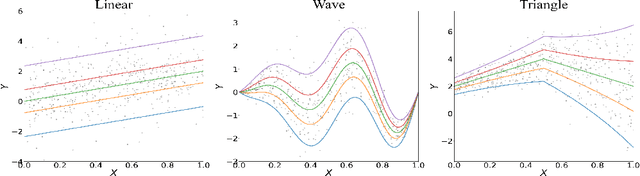
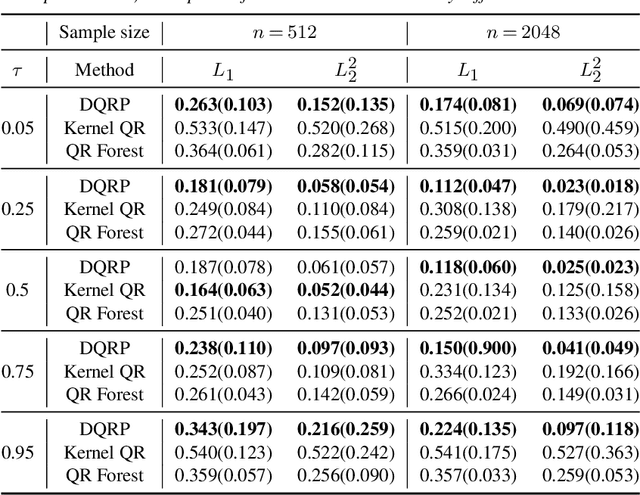
We propose a penalized nonparametric approach to estimating the quantile regression process (QRP) in a nonseparable model using rectifier quadratic unit (ReQU) activated deep neural networks and introduce a novel penalty function to enforce non-crossing of quantile regression curves. We establish the non-asymptotic excess risk bounds for the estimated QRP and derive the mean integrated squared error for the estimated QRP under mild smoothness and regularity conditions. To establish these non-asymptotic risk and estimation error bounds, we also develop a new error bound for approximating $C^s$ smooth functions with $s >0$ and their derivatives using ReQU activated neural networks. This is a new approximation result for ReQU networks and is of independent interest and may be useful in other problems. Our numerical experiments demonstrate that the proposed method is competitive with or outperforms two existing methods, including methods using reproducing kernels and random forests, for nonparametric quantile regression.

Non-asymptotic Excess Risk Bounds for Classification with Deep Convolutional Neural Networks

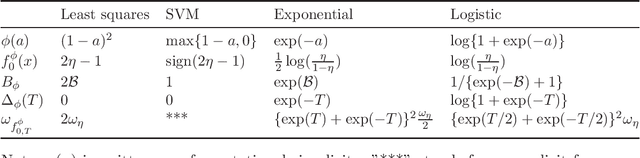
In this paper, we consider the problem of binary classification with a class of general deep convolutional neural networks, which includes fully-connected neural networks and fully convolutional neural networks as special cases. We establish non-asymptotic excess risk bounds for a class of convex surrogate losses and target functions with different modulus of continuity. An important feature of our results is that we clearly define the prefactors of the risk bounds in terms of the input data dimension and other model parameters and show that they depend polynomially on the dimensionality in some important models. We also show that the classification methods with CNNs can circumvent the curse of dimensionality if the input data is supported on an approximate low-dimensional manifold. To establish these results, we derive an upper bound for the covering number for the class of general convolutional neural networks with a bias term in each convolutional layer, and derive new results on the approximation power of CNNs for any uniformly-continuous target functions. These results provide further insights into the complexity and the approximation power of general convolutional neural networks, which are of independent interest and may have other applications. Finally, we apply our general results to analyze the non-asymptotic excess risk bounds for four widely used methods with different loss functions using CNNs, including the least squares, the logistic, the exponential and the SVM hinge losses.