Conditional Stochastic Interpolation for Generative Learning
Paper and Code
Dec 09, 2023
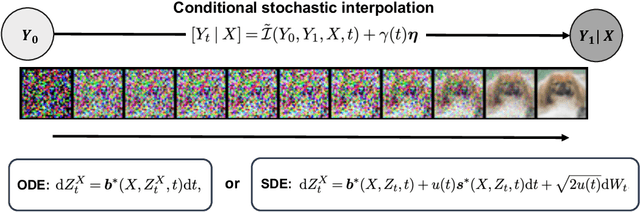
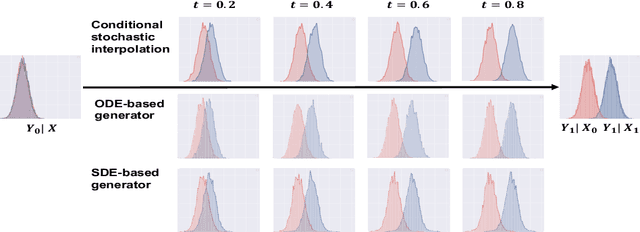

We propose a conditional stochastic interpolation (CSI) approach to learning conditional distributions. CSI learns probability flow equations or stochastic differential equations that transport a reference distribution to the target conditional distribution. This is achieved by first learning the drift function and the conditional score function based on conditional stochastic interpolation, which are then used to construct a deterministic process governed by an ordinary differential equation or a diffusion process for conditional sampling. In our proposed CSI model, we incorporate an adaptive diffusion term to address the instability issues arising during the training process. We provide explicit forms of the conditional score function and the drift function in terms of conditional expectations under mild conditions, which naturally lead to an nonparametric regression approach to estimating these functions. Furthermore, we establish non-asymptotic error bounds for learning the target conditional distribution via conditional stochastic interpolation in terms of KL divergence, taking into account the neural network approximation error. We illustrate the application of CSI on image generation using a benchmark image dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge