A robust assessment for invariant representations

The performance of machine learning models can be impacted by changes in data over time. A promising approach to address this challenge is invariant learning, with a particular focus on a method known as invariant risk minimization (IRM). This technique aims to identify a stable data representation that remains effective with out-of-distribution (OOD) data. While numerous studies have developed IRM-based methods adaptive to data augmentation scenarios, there has been limited attention on directly assessing how well these representations preserve their invariant performance under varying conditions. In our paper, we propose a novel method to evaluate invariant performance, specifically tailored for IRM-based methods. We establish a bridge between the conditional expectation of an invariant predictor across different environments through the likelihood ratio. Our proposed criterion offers a robust basis for evaluating invariant performance. We validate our approach with theoretical support and demonstrate its effectiveness through extensive numerical studies.These experiments illustrate how our method can assess the invariant performance of various representation techniques.

Statistical inference for pairwise comparison models

Pairwise comparison models are used for quantitatively evaluating utility and ranking in various fields. The increasing scale of modern problems underscores the need to understand statistical inference in these models when the number of subjects diverges, which is currently lacking in the literature except in a few special instances. This paper addresses this gap by establishing an asymptotic normality result for the maximum likelihood estimator in a broad class of pairwise comparison models. The key idea lies in identifying the Fisher information matrix as a weighted graph Laplacian matrix which can be studied via a meticulous spectral analysis. Our findings provide the first unified theory for performing statistical inference in a wide range of pairwise comparison models beyond the Bradley--Terry model, benefiting practitioners with a solid theoretical guarantee for their use. Simulations utilizing synthetic data are conducted to validate the asymptotic normality result, followed by a hypothesis test using a tennis competition dataset.

Conformal Inference for Invariant Risk Minimization

The application of machine learning models can be significantly impeded by the occurrence of distributional shifts, as the assumption of homogeneity between the population of training and testing samples in machine learning and statistics may not be feasible in practical situations. One way to tackle this problem is to use invariant learning, such as invariant risk minimization (IRM), to acquire an invariant representation that aids in generalization with distributional shifts. This paper develops methods for obtaining distribution-free prediction regions to describe uncertainty estimates for invariant representations, accounting for the distribution shifts of data from different environments. Our approach involves a weighted conformity score that adapts to the specific environment in which the test sample is situated. We construct an adaptive conformal interval using the weighted conformity score and prove its conditional average under certain conditions. To demonstrate the effectiveness of our approach, we conduct several numerical experiments, including simulation studies and a practical example using real-world data.

Nonparametric Quantile Regression: Non-Crossing Constraints and Conformal Prediction

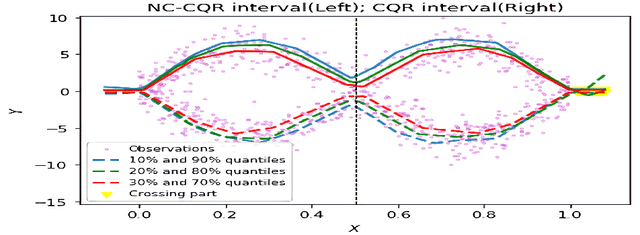
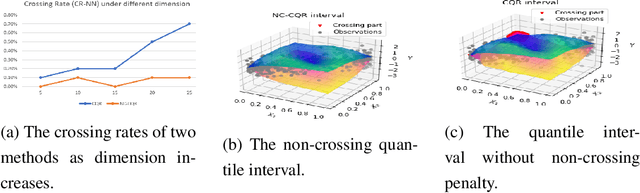
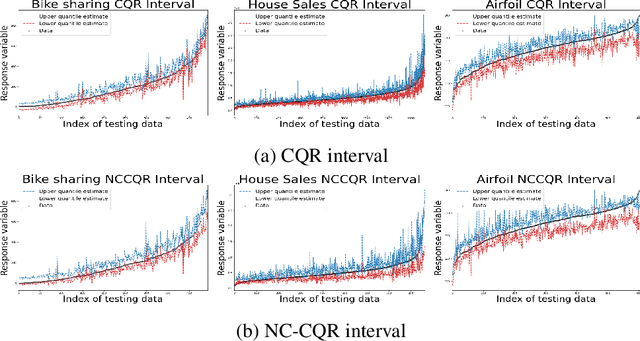
We propose a nonparametric quantile regression method using deep neural networks with a rectified linear unit penalty function to avoid quantile crossing. This penalty function is computationally feasible for enforcing non-crossing constraints in multi-dimensional nonparametric quantile regression. We establish non-asymptotic upper bounds for the excess risk of the proposed nonparametric quantile regression function estimators. Our error bounds achieve optimal minimax rate of convergence for the Holder class, and the prefactors of the error bounds depend polynomially on the dimension of the predictor, instead of exponentially. Based on the proposed non-crossing penalized deep quantile regression, we construct conformal prediction intervals that are fully adaptive to heterogeneity. The proposed prediction interval is shown to have good properties in terms of validity and accuracy under reasonable conditions. We also derive non-asymptotic upper bounds for the difference of the lengths between the proposed non-crossing conformal prediction interval and the theoretically oracle prediction interval. Numerical experiments including simulation studies and a real data example are conducted to demonstrate the effectiveness of the proposed method.