OCDB: Revisiting Causal Discovery with a Comprehensive Benchmark and Evaluation Framework

Large language models (LLMs) have excelled in various natural language processing tasks, but challenges in interpretability and trustworthiness persist, limiting their use in high-stakes fields. Causal discovery offers a promising approach to improve transparency and reliability. However, current evaluations are often one-sided and lack assessments focused on interpretability performance. Additionally, these evaluations rely on synthetic data and lack comprehensive assessments of real-world datasets. These lead to promising methods potentially being overlooked. To address these issues, we propose a flexible evaluation framework with metrics for evaluating differences in causal structures and causal effects, which are crucial attributes that help improve the interpretability of LLMs. We introduce the Open Causal Discovery Benchmark (OCDB), based on real data, to promote fair comparisons and drive optimization of algorithms. Additionally, our new metrics account for undirected edges, enabling fair comparisons between Directed Acyclic Graphs (DAGs) and Completed Partially Directed Acyclic Graphs (CPDAGs). Experimental results show significant shortcomings in existing algorithms' generalization capabilities on real data, highlighting the potential for performance improvement and the importance of our framework in advancing causal discovery techniques.

Adaptive debiased SGD in high-dimensional GLMs with steaming data

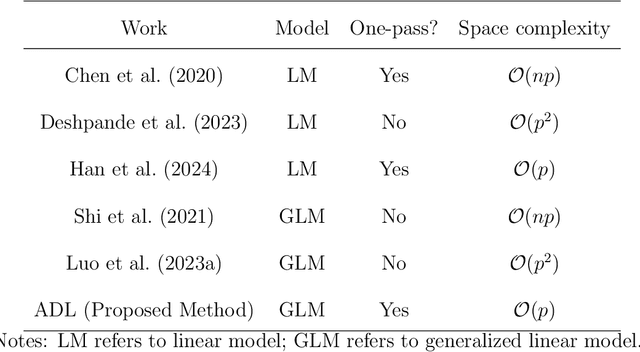
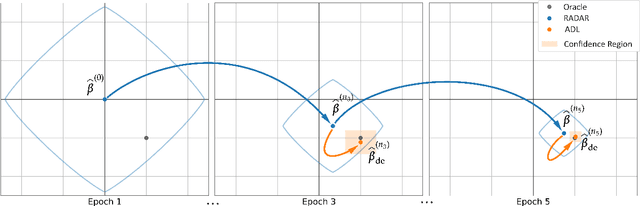
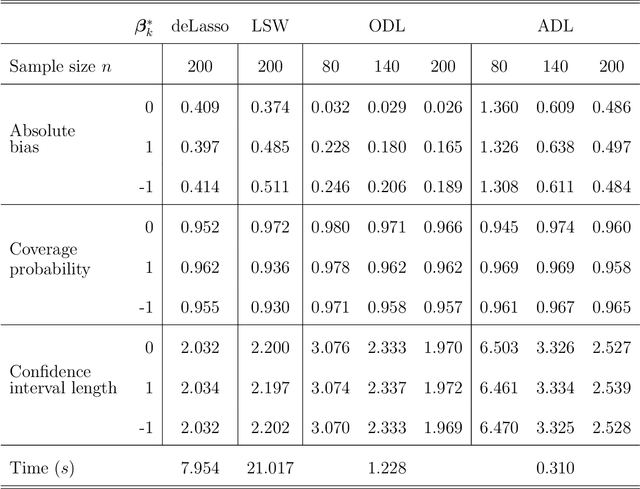
Online statistical inference facilitates real-time analysis of sequentially collected data, making it different from traditional methods that rely on static datasets. This paper introduces a novel approach to online inference in high-dimensional generalized linear models, where we update regression coefficient estimates and their standard errors upon each new data arrival. In contrast to existing methods that either require full dataset access or large-dimensional summary statistics storage, our method operates in a single-pass mode, significantly reducing both time and space complexity. The core of our methodological innovation lies in an adaptive stochastic gradient descent algorithm tailored for dynamic objective functions, coupled with a novel online debiasing procedure. This allows us to maintain low-dimensional summary statistics while effectively controlling optimization errors introduced by the dynamically changing loss functions. We demonstrate that our method, termed the Approximated Debiased Lasso (ADL), not only mitigates the need for the bounded individual probability condition but also significantly improves numerical performance. Numerical experiments demonstrate that the proposed ADL method consistently exhibits robust performance across various covariance matrix structures.

Efficient semi-supervised inference for logistic regression under case-control studies

Semi-supervised learning has received increasingly attention in statistics and machine learning. In semi-supervised learning settings, a labeled data set with both outcomes and covariates and an unlabeled data set with covariates only are collected. We consider an inference problem in semi-supervised settings where the outcome in the labeled data is binary and the labeled data is collected by case-control sampling. Case-control sampling is an effective sampling scheme for alleviating imbalance structure in binary data. Under the logistic model assumption, case-control data can still provide consistent estimator for the slope parameter of the regression model. However, the intercept parameter is not identifiable. Consequently, the marginal case proportion cannot be estimated from case-control data. We find out that with the availability of the unlabeled data, the intercept parameter can be identified in semi-supervised learning setting. We construct the likelihood function of the observed labeled and unlabeled data and obtain the maximum likelihood estimator via an iterative algorithm. The proposed estimator is shown to be consistent, asymptotically normal, and semiparametrically efficient. Extensive simulation studies are conducted to show the finite sample performance of the proposed method. The results imply that the unlabeled data not only helps to identify the intercept but also improves the estimation efficiency of the slope parameter. Meanwhile, the marginal case proportion can be estimated accurately by the proposed method.

Wasserstein Generative Regression

In this paper, we propose a new and unified approach for nonparametric regression and conditional distribution learning. Our approach simultaneously estimates a regression function and a conditional generator using a generative learning framework, where a conditional generator is a function that can generate samples from a conditional distribution. The main idea is to estimate a conditional generator that satisfies the constraint that it produces a good regression function estimator. We use deep neural networks to model the conditional generator. Our approach can handle problems with multivariate outcomes and covariates, and can be used to construct prediction intervals. We provide theoretical guarantees by deriving non-asymptotic error bounds and the distributional consistency of our approach under suitable assumptions. We also perform numerical experiments with simulated and real data to demonstrate the effectiveness and superiority of our approach over some existing approaches in various scenarios.

Differentiable Neural Networks with RePU Activation: with Applications to Score Estimation and Isotonic Regression

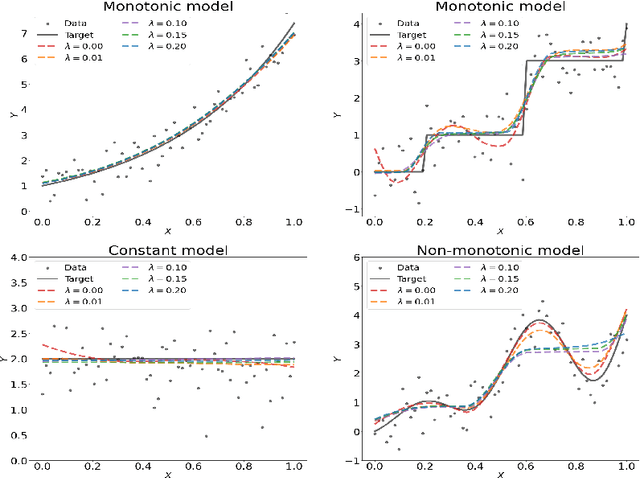
We study the properties of differentiable neural networks activated by rectified power unit (RePU) functions. We show that the partial derivatives of RePU neural networks can be represented by RePUs mixed-activated networks and derive upper bounds for the complexity of the function class of derivatives of RePUs networks. We establish error bounds for simultaneously approximating $C^s$ smooth functions and their derivatives using RePU-activated deep neural networks. Furthermore, we derive improved approximation error bounds when data has an approximate low-dimensional support, demonstrating the ability of RePU networks to mitigate the curse of dimensionality. To illustrate the usefulness of our results, we consider a deep score matching estimator (DSME) and propose a penalized deep isotonic regression (PDIR) using RePU networks. We establish non-asymptotic excess risk bounds for DSME and PDIR under the assumption that the target functions belong to a class of $C^s$ smooth functions. We also show that PDIR has a robustness property in the sense it is consistent with vanishing penalty parameters even when the monotonicity assumption is not satisfied. Furthermore, if the data distribution is supported on an approximate low-dimensional manifold, we show that DSME and PDIR can mitigate the curse of dimensionality.

Nonparametric Quantile Regression: Non-Crossing Constraints and Conformal Prediction

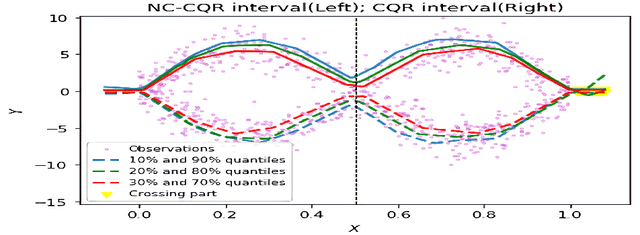
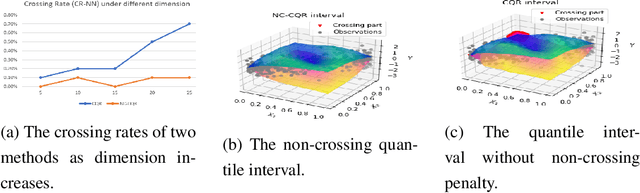
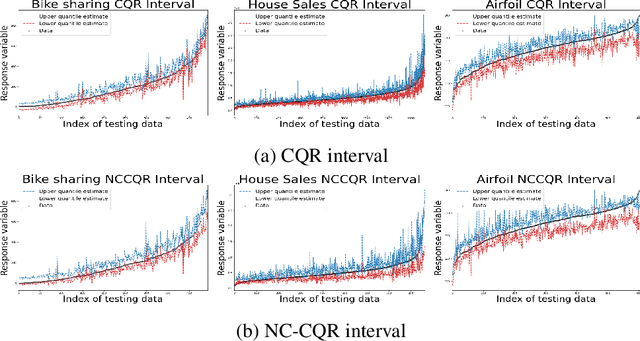
We propose a nonparametric quantile regression method using deep neural networks with a rectified linear unit penalty function to avoid quantile crossing. This penalty function is computationally feasible for enforcing non-crossing constraints in multi-dimensional nonparametric quantile regression. We establish non-asymptotic upper bounds for the excess risk of the proposed nonparametric quantile regression function estimators. Our error bounds achieve optimal minimax rate of convergence for the Holder class, and the prefactors of the error bounds depend polynomially on the dimension of the predictor, instead of exponentially. Based on the proposed non-crossing penalized deep quantile regression, we construct conformal prediction intervals that are fully adaptive to heterogeneity. The proposed prediction interval is shown to have good properties in terms of validity and accuracy under reasonable conditions. We also derive non-asymptotic upper bounds for the difference of the lengths between the proposed non-crossing conformal prediction interval and the theoretically oracle prediction interval. Numerical experiments including simulation studies and a real data example are conducted to demonstrate the effectiveness of the proposed method.

Deep Sufficient Representation Learning via Mutual Information

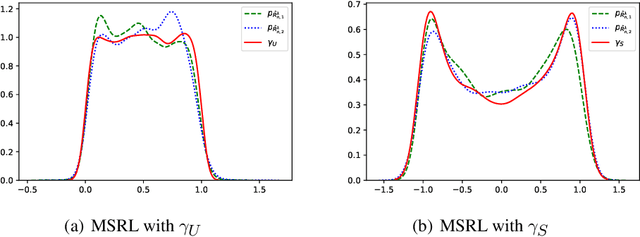
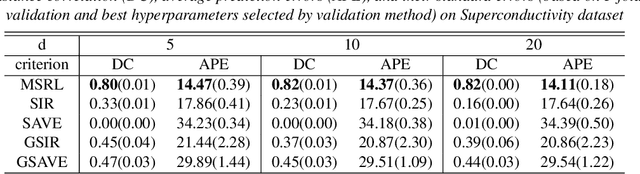
We propose a mutual information-based sufficient representation learning (MSRL) approach, which uses the variational formulation of the mutual information and leverages the approximation power of deep neural networks. MSRL learns a sufficient representation with the maximum mutual information with the response and a user-selected distribution. It can easily handle multi-dimensional continuous or categorical response variables. MSRL is shown to be consistent in the sense that the conditional probability density function of the response variable given the learned representation converges to the conditional probability density function of the response variable given the predictor. Non-asymptotic error bounds for MSRL are also established under suitable conditions. To establish the error bounds, we derive a generalized Dudley's inequality for an order-two U-process indexed by deep neural networks, which may be of independent interest. We discuss how to determine the intrinsic dimension of the underlying data distribution. Moreover, we evaluate the performance of MSRL via extensive numerical experiments and real data analysis and demonstrate that MSRL outperforms some existing nonlinear sufficient dimension reduction methods.

Estimation of Non-Crossing Quantile Regression Process with Deep ReQU Neural Networks

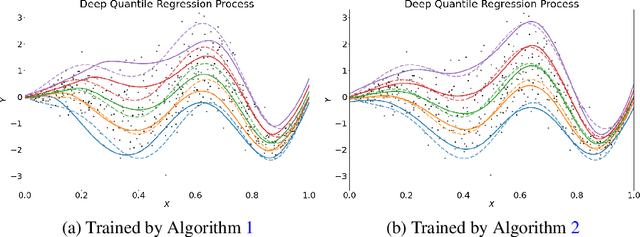
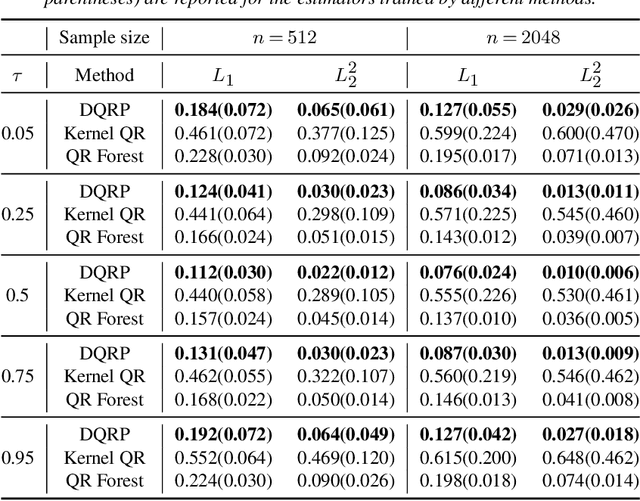
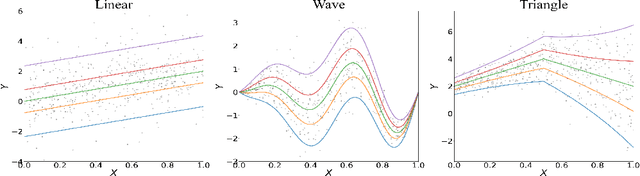
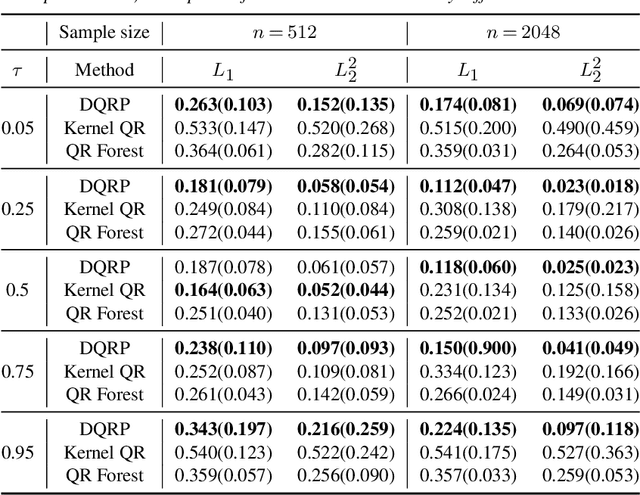
We propose a penalized nonparametric approach to estimating the quantile regression process (QRP) in a nonseparable model using rectifier quadratic unit (ReQU) activated deep neural networks and introduce a novel penalty function to enforce non-crossing of quantile regression curves. We establish the non-asymptotic excess risk bounds for the estimated QRP and derive the mean integrated squared error for the estimated QRP under mild smoothness and regularity conditions. To establish these non-asymptotic risk and estimation error bounds, we also develop a new error bound for approximating $C^s$ smooth functions with $s >0$ and their derivatives using ReQU activated neural networks. This is a new approximation result for ReQU networks and is of independent interest and may be useful in other problems. Our numerical experiments demonstrate that the proposed method is competitive with or outperforms two existing methods, including methods using reproducing kernels and random forests, for nonparametric quantile regression.

Non-asymptotic Excess Risk Bounds for Classification with Deep Convolutional Neural Networks

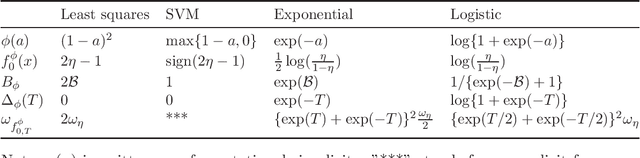
In this paper, we consider the problem of binary classification with a class of general deep convolutional neural networks, which includes fully-connected neural networks and fully convolutional neural networks as special cases. We establish non-asymptotic excess risk bounds for a class of convex surrogate losses and target functions with different modulus of continuity. An important feature of our results is that we clearly define the prefactors of the risk bounds in terms of the input data dimension and other model parameters and show that they depend polynomially on the dimensionality in some important models. We also show that the classification methods with CNNs can circumvent the curse of dimensionality if the input data is supported on an approximate low-dimensional manifold. To establish these results, we derive an upper bound for the covering number for the class of general convolutional neural networks with a bias term in each convolutional layer, and derive new results on the approximation power of CNNs for any uniformly-continuous target functions. These results provide further insights into the complexity and the approximation power of general convolutional neural networks, which are of independent interest and may have other applications. Finally, we apply our general results to analyze the non-asymptotic excess risk bounds for four widely used methods with different loss functions using CNNs, including the least squares, the logistic, the exponential and the SVM hinge losses.