Deep Sufficient Representation Learning via Mutual Information
Paper and Code
Jul 21, 2022
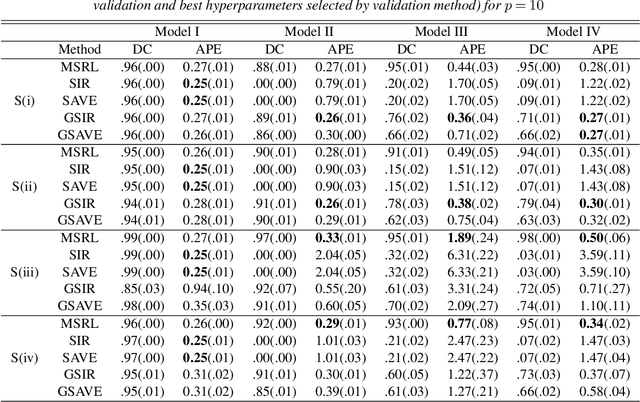
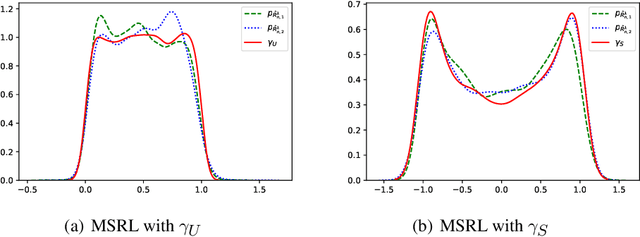
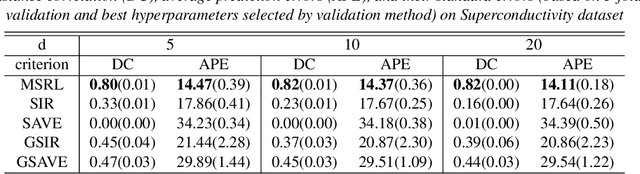
We propose a mutual information-based sufficient representation learning (MSRL) approach, which uses the variational formulation of the mutual information and leverages the approximation power of deep neural networks. MSRL learns a sufficient representation with the maximum mutual information with the response and a user-selected distribution. It can easily handle multi-dimensional continuous or categorical response variables. MSRL is shown to be consistent in the sense that the conditional probability density function of the response variable given the learned representation converges to the conditional probability density function of the response variable given the predictor. Non-asymptotic error bounds for MSRL are also established under suitable conditions. To establish the error bounds, we derive a generalized Dudley's inequality for an order-two U-process indexed by deep neural networks, which may be of independent interest. We discuss how to determine the intrinsic dimension of the underlying data distribution. Moreover, we evaluate the performance of MSRL via extensive numerical experiments and real data analysis and demonstrate that MSRL outperforms some existing nonlinear sufficient dimension reduction methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge