A General Pairwise Comparison Model for Extremely Sparse Networks
Paper and Code
Feb 20, 2020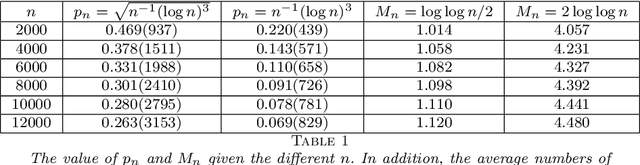
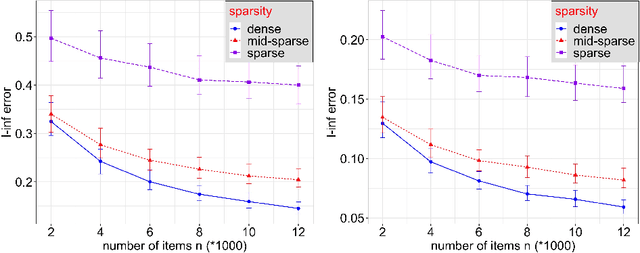
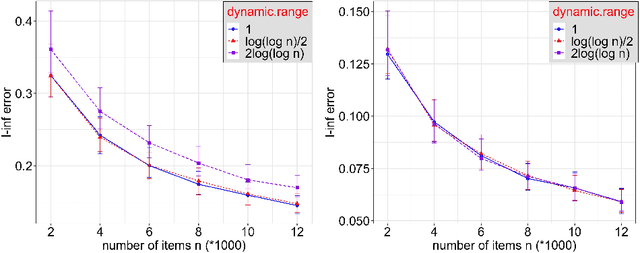
Statistical inference using pairwise comparison data has been an effective approach to analyzing complex and sparse networks. In this paper we propose a general framework for modeling the mutual interaction in a probabilistic network, which enjoys ample flexibility in terms of parametrization. Within this set-up, we establish that the maximum likelihood estimator (MLE) for the latent scores of the subjects is uniformly consistent under a near-minimal condition on network sparsity. This condition is sharp in terms of the leading order asymptotics describing the sparsity. The proof utilizes a novel chaining technique based on the error-induced metric as well as careful counting of comparison graph structures. Our results guarantee that the MLE is a valid estimator for inference in large-scale comparison networks where data is asymptotically deficient. Numerical simulations are provided to complement the theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge