DARE: Aligning LLM Agents with the R Statistical Ecosystem via Distribution-Aware Retrieval

Large Language Model (LLM) agents can automate data-science workflows, but many rigorous statistical methods implemented in R remain underused because LLMs struggle with statistical knowledge and tool retrieval. Existing retrieval-augmented approaches focus on function-level semantics and ignore data distribution, producing suboptimal matches. We propose DARE (Distribution-Aware Retrieval Embedding), a lightweight, plug-and-play retrieval model that incorporates data distribution information into function representations for R package retrieval. Our main contributions are: (i) RPKB, a curated R Package Knowledge Base derived from 8,191 high-quality CRAN packages; (ii) DARE, an embedding model that fuses distributional features with function metadata to improve retrieval relevance; and (iii) RCodingAgent, an R-oriented LLM agent for reliable R code generation and a suite of statistical analysis tasks for systematically evaluating LLM agents in realistic analytical scenarios. Empirically, DARE achieves an NDCG at 10 of 93.47%, outperforming state-of-the-art open-source embedding models by up to 17% on package retrieval while using substantially fewer parameters. Integrating DARE into RCodingAgent yields significant gains on downstream analysis tasks. This work helps narrow the gap between LLM automation and the mature R statistical ecosystem.

LLM-Enhanced Rumor Detection via Virtual Node Induced Edge Prediction

The proliferation of rumors on social networks undermines information credibility. While their dissemination forms complex networks, current detection methods struggle to capture these intricate propagation patterns. Representing each node solely through its textual embeddings neglects the textual coherence across the entire rumor propagation path, which compromises the accuracy of rumor identification on social platforms. We propose a novel framework that leverages Large Language Models (LLMs) to address these limitations. Our approach captures subtle rumor signals by employing LLMs to analyze information subchains, assign rumor probabilities and intelligently construct connections to virtual nodes. This enables the modification of the original graph structure, which is a critical advancement for capturing subtle rumor signals. Given the inherent limitations of LLMs in rumor identification, we develop a structured prompt framework to mitigate model biases and ensure robust graph learning performance. Additionally, the proposed framework is model-agnostic, meaning it is not constrained to any specific graph learning algorithm or LLMs. Its plug-and-play nature allows for seamless integration with further fine-tuned LLMs and graph techniques in the future, potentially enhancing predictive performance without modifying original algorithms.

DSAEval: Evaluating Data Science Agents on a Wide Range of Real-World Data Science Problems

Recent LLM-based data agents aim to automate data science tasks ranging from data analysis to deep learning. However, the open-ended nature of real-world data science problems, which often span multiple taxonomies and lack standard answers, poses a significant challenge for evaluation. To address this, we introduce DSAEval, a benchmark comprising 641 real-world data science problems grounded in 285 diverse datasets, covering both structured and unstructured data (e.g., vision and text). DSAEval incorporates three distinctive features: (1) Multimodal Environment Perception, which enables agents to interpret observations from multiple modalities including text and vision; (2) Multi-Query Interactions, which mirror the iterative and cumulative nature of real-world data science projects; and (3) Multi-Dimensional Evaluation, which provides a holistic assessment across reasoning, code, and results. We systematically evaluate 11 advanced agentic LLMs using DSAEval. Our results show that Claude-Sonnet-4.5 achieves the strongest overall performance, GPT-5.2 is the most efficient, and MiMo-V2-Flash is the most cost-effective. We further demonstrate that multimodal perception consistently improves performance on vision-related tasks, with gains ranging from 2.04% to 11.30%. Overall, while current data science agents perform well on structured data and routine data anlysis workflows, substantial challenges remain in unstructured domains. Finally, we offer critical insights and outline future research directions to advance the development of data science agents.

A Survey on Large Language Model-based Agents for Statistics and Data Science

In recent years, data science agents powered by Large Language Models (LLMs), known as "data agents," have shown significant potential to transform the traditional data analysis paradigm. This survey provides an overview of the evolution, capabilities, and applications of LLM-based data agents, highlighting their role in simplifying complex data tasks and lowering the entry barrier for users without related expertise. We explore current trends in the design of LLM-based frameworks, detailing essential features such as planning, reasoning, reflection, multi-agent collaboration, user interface, knowledge integration, and system design, which enable agents to address data-centric problems with minimal human intervention. Furthermore, we analyze several case studies to demonstrate the practical applications of various data agents in real-world scenarios. Finally, we identify key challenges and propose future research directions to advance the development of data agents into intelligent statistical analysis software.

LAMBDA: A Large Model Based Data Agent

We introduce ``LAMBDA," a novel open-source, code-free multi-agent data analysis system that that harnesses the power of large models. LAMBDA is designed to address data analysis challenges in complex data-driven applications through the use of innovatively designed data agents that operate iteratively and generatively using natural language. At the core of LAMBDA are two key agent roles: the programmer and the inspector, which are engineered to work together seamlessly. Specifically, the programmer generates code based on the user's instructions and domain-specific knowledge, enhanced by advanced models. Meanwhile, the inspector debugs the code when necessary. To ensure robustness and handle adverse scenarios, LAMBDA features a user interface that allows direct user intervention in the operational loop. Additionally, LAMBDA can flexibly integrate external models and algorithms through our knowledge integration mechanism, catering to the needs of customized data analysis. LAMBDA has demonstrated strong performance on various machine learning datasets. It has the potential to enhance data science practice and analysis paradigm by seamlessly integrating human and artificial intelligence, making it more accessible, effective, and efficient for individuals from diverse backgrounds. The strong performance of LAMBDA in solving data science problems is demonstrated in several case studies, which are presented at \url{https://www.polyu.edu.hk/ama/cmfai/lambda.html}.

Statistical ranking with dynamic covariates

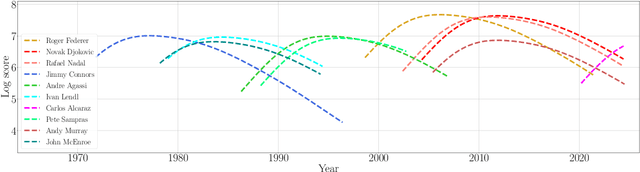
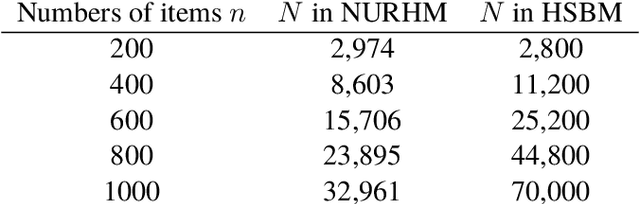
We consider a covariate-assisted ranking model grounded in the Plackett--Luce framework. Unlike existing works focusing on pure covariates or individual effects with fixed covariates, our approach integrates individual effects with dynamic covariates. This added flexibility enhances realistic ranking yet poses significant challenges for analyzing the associated estimation procedures. This paper makes an initial attempt to address these challenges. We begin by discussing the sufficient and necessary condition for the model's identifiability. We then introduce an efficient alternating maximization algorithm to compute the maximum likelihood estimator (MLE). Under suitable assumptions on the topology of comparison graphs and dynamic covariates, we establish a quantitative uniform consistency result for the MLE with convergence rates characterized by the asymptotic graph connectivity. The proposed graph topology assumption holds for several popular random graph models under optimal leading-order sparsity conditions. A comprehensive numerical study is conducted to corroborate our theoretical findings and demonstrate the application of the proposed model to real-world datasets, including horse racing and tennis competitions.

Linear Discriminant Analysis with High-dimensional Mixed Variables

Datasets containing both categorical and continuous variables are frequently encountered in many areas, and with the rapid development of modern measurement technologies, the dimensions of these variables can be very high. Despite the recent progress made in modelling high-dimensional data for continuous variables, there is a scarcity of methods that can deal with a mixed set of variables. To fill this gap, this paper develops a novel approach for classifying high-dimensional observations with mixed variables. Our framework builds on a location model, in which the distributions of the continuous variables conditional on categorical ones are assumed Gaussian. We overcome the challenge of having to split data into exponentially many cells, or combinations of the categorical variables, by kernel smoothing, and provide new perspectives for its bandwidth choice to ensure an analogue of Bochner's Lemma, which is different to the usual bias-variance tradeoff. We show that the two sets of parameters in our model can be separately estimated and provide penalized likelihood for their estimation. Results on the estimation accuracy and the misclassification rates are established, and the competitive performance of the proposed classifier is illustrated by extensive simulation and real data studies.

A Direct Approach for Sparse Quadratic Discriminant Analysis

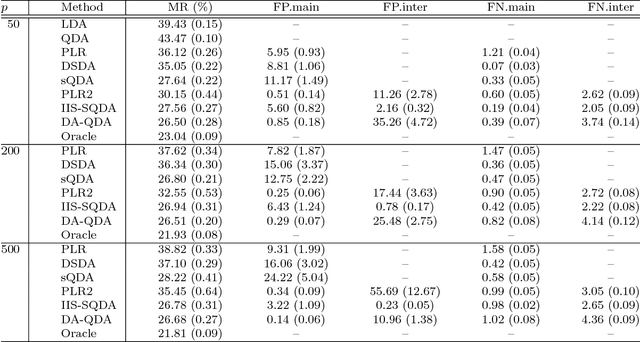
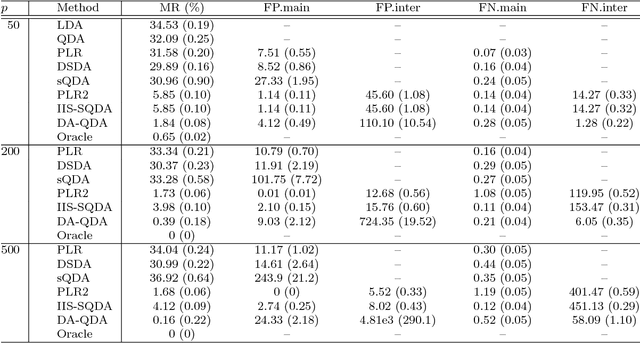
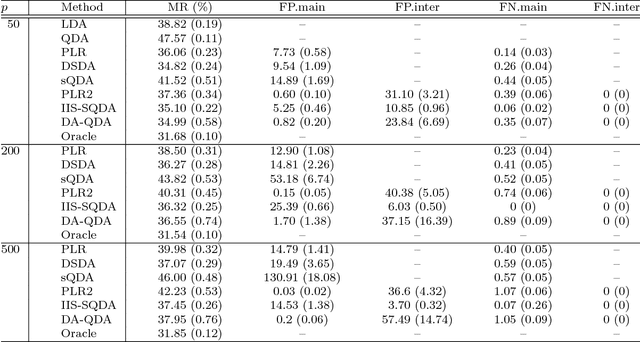
Quadratic discriminant analysis (QDA) is a standard tool for classification due to its simplicity and flexibility. Because the number of its parameters scales quadratically with the number of the variables, QDA is not practical, however, when the dimensionality is relatively large. To address this, we propose a novel procedure named DA-QDA for QDA in analyzing high-dimensional data. Formulated in a simple and coherent framework, DA-QDA aims to directly estimate the key quantities in the Bayes discriminant function including quadratic interactions and a linear index of the variables for classification. Under appropriate sparsity assumptions, we establish consistency results for estimating the interactions and the linear index, and further demonstrate that the misclassification rate of our procedure converges to the optimal Bayes risk, even when the dimensionality is exponentially high with respect to the sample size. An efficient algorithm based on the alternating direction method of multipliers (ADMM) is developed for finding interactions, which is much faster than its competitor in the literature. The promising performance of DA-QDA is illustrated via extensive simulation studies and the analysis of four real datasets.