Linear Discriminant Analysis with High-dimensional Mixed Variables

Datasets containing both categorical and continuous variables are frequently encountered in many areas, and with the rapid development of modern measurement technologies, the dimensions of these variables can be very high. Despite the recent progress made in modelling high-dimensional data for continuous variables, there is a scarcity of methods that can deal with a mixed set of variables. To fill this gap, this paper develops a novel approach for classifying high-dimensional observations with mixed variables. Our framework builds on a location model, in which the distributions of the continuous variables conditional on categorical ones are assumed Gaussian. We overcome the challenge of having to split data into exponentially many cells, or combinations of the categorical variables, by kernel smoothing, and provide new perspectives for its bandwidth choice to ensure an analogue of Bochner's Lemma, which is different to the usual bias-variance tradeoff. We show that the two sets of parameters in our model can be separately estimated and provide penalized likelihood for their estimation. Results on the estimation accuracy and the misclassification rates are established, and the competitive performance of the proposed classifier is illustrated by extensive simulation and real data studies.

A Direct Approach for Sparse Quadratic Discriminant Analysis

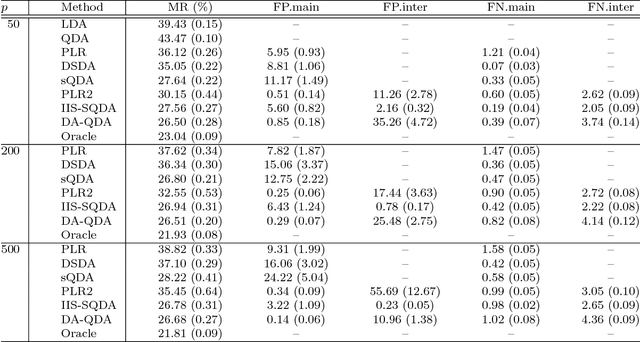
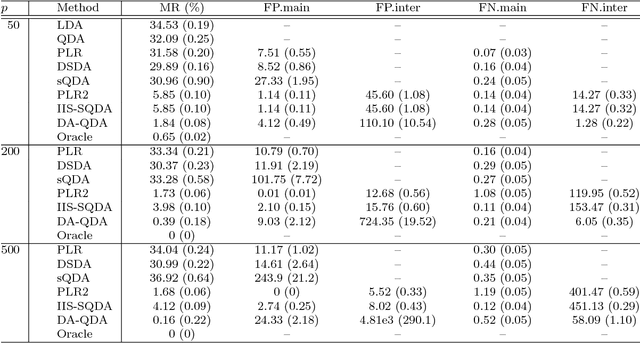
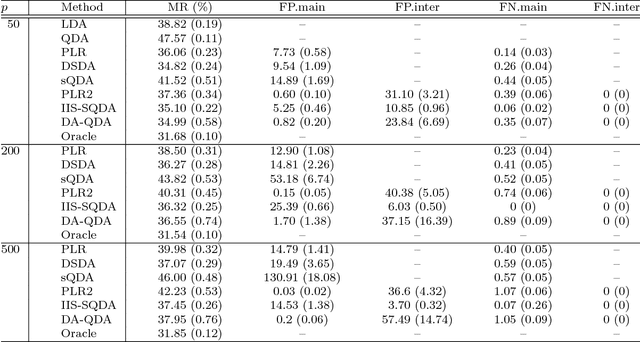
Quadratic discriminant analysis (QDA) is a standard tool for classification due to its simplicity and flexibility. Because the number of its parameters scales quadratically with the number of the variables, QDA is not practical, however, when the dimensionality is relatively large. To address this, we propose a novel procedure named DA-QDA for QDA in analyzing high-dimensional data. Formulated in a simple and coherent framework, DA-QDA aims to directly estimate the key quantities in the Bayes discriminant function including quadratic interactions and a linear index of the variables for classification. Under appropriate sparsity assumptions, we establish consistency results for estimating the interactions and the linear index, and further demonstrate that the misclassification rate of our procedure converges to the optimal Bayes risk, even when the dimensionality is exponentially high with respect to the sample size. An efficient algorithm based on the alternating direction method of multipliers (ADMM) is developed for finding interactions, which is much faster than its competitor in the literature. The promising performance of DA-QDA is illustrated via extensive simulation studies and the analysis of four real datasets.

No penalty no tears: Least squares in high-dimensional linear models

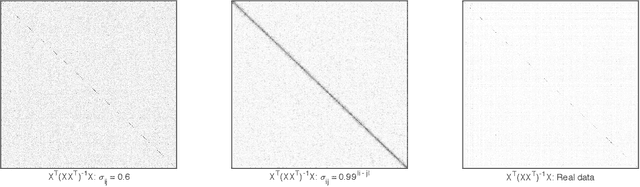
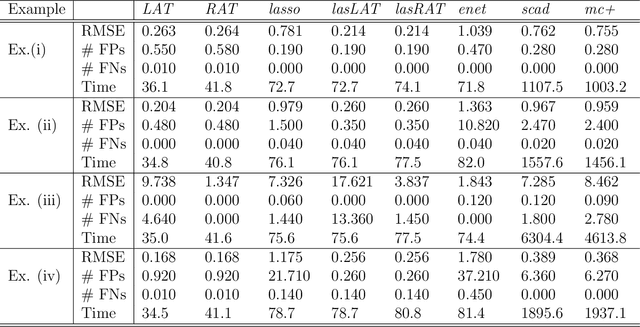
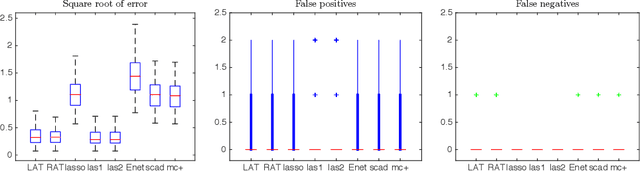
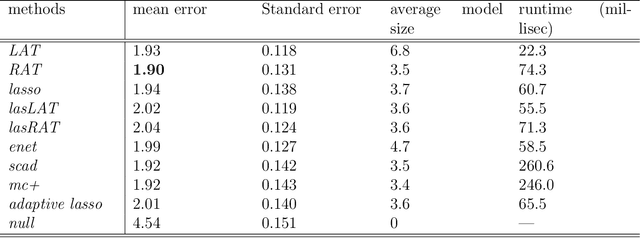
Ordinary least squares (OLS) is the default method for fitting linear models, but is not applicable for problems with dimensionality larger than the sample size. For these problems, we advocate the use of a generalized version of OLS motivated by ridge regression, and propose two novel three-step algorithms involving least squares fitting and hard thresholding. The algorithms are methodologically simple to understand intuitively, computationally easy to implement efficiently, and theoretically appealing for choosing models consistently. Numerical exercises comparing our methods with penalization-based approaches in simulations and data analyses illustrate the great potential of the proposed algorithms.

DECOrrelated feature space partitioning for distributed sparse regression

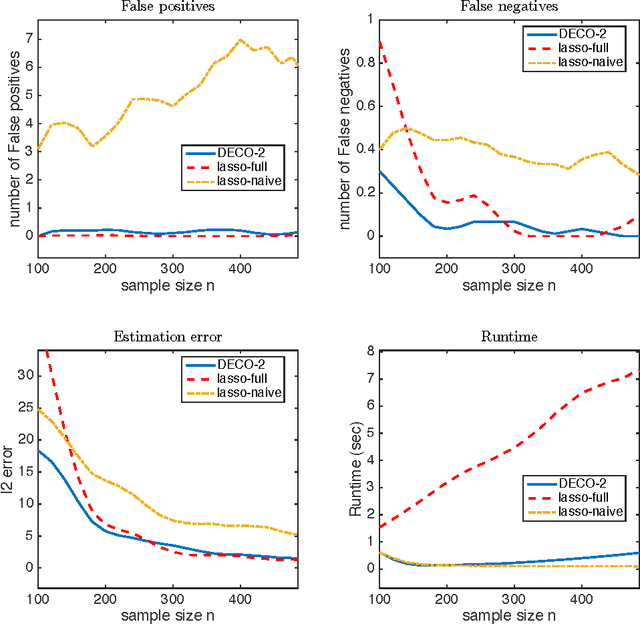
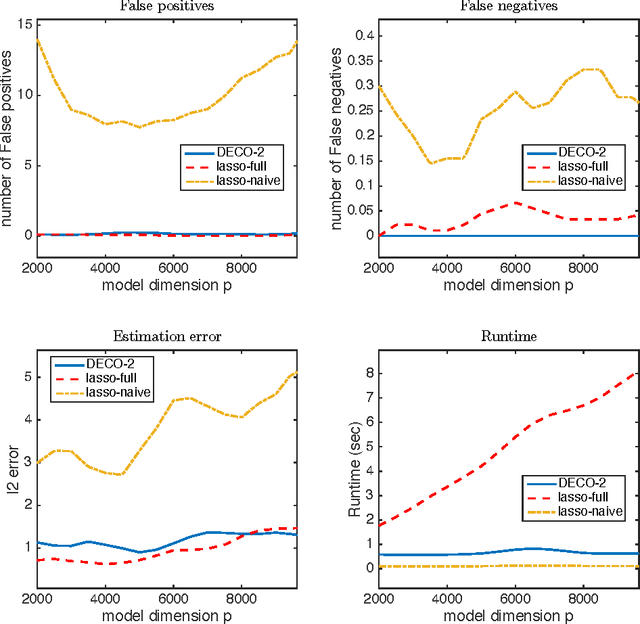
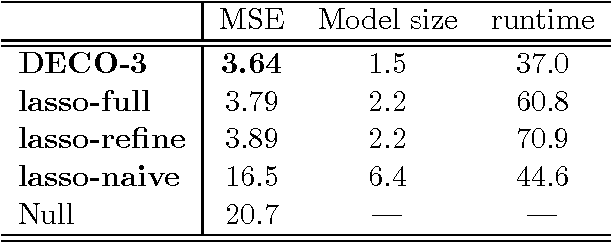
Fitting statistical models is computationally challenging when the sample size or the dimension of the dataset is huge. An attractive approach for down-scaling the problem size is to first partition the dataset into subsets and then fit using distributed algorithms. The dataset can be partitioned either horizontally (in the sample space) or vertically (in the feature space). While the majority of the literature focuses on sample space partitioning, feature space partitioning is more effective when $p\gg n$. Existing methods for partitioning features, however, are either vulnerable to high correlations or inefficient in reducing the model dimension. In this paper, we solve these problems through a new embarrassingly parallel framework named DECO for distributed variable selection and parameter estimation. In DECO, variables are first partitioned and allocated to $m$ distributed workers. The decorrelated subset data within each worker are then fitted via any algorithm designed for high-dimensional problems. We show that by incorporating the decorrelation step, DECO can achieve consistent variable selection and parameter estimation on each subset with (almost) no assumptions. In addition, the convergence rate is nearly minimax optimal for both sparse and weakly sparse models and does NOT depend on the partition number $m$. Extensive numerical experiments are provided to illustrate the performance of the new framework.

On the consistency theory of high dimensional variable screening

Variable screening is a fast dimension reduction technique for assisting high dimensional feature selection. As a preselection method, it selects a moderate size subset of candidate variables for further refining via feature selection to produce the final model. The performance of variable screening depends on both computational efficiency and the ability to dramatically reduce the number of variables without discarding the important ones. When the data dimension $p$ is substantially larger than the sample size $n$, variable screening becomes crucial as 1) Faster feature selection algorithms are needed; 2) Conditions guaranteeing selection consistency might fail to hold. This article studies a class of linear screening methods and establishes consistency theory for this special class. In particular, we prove the restricted diagonally dominant (RDD) condition is a necessary and sufficient condition for strong screening consistency. As concrete examples, we show two screening methods $SIS$ and $HOLP$ are both strong screening consistent (subject to additional constraints) with large probability if $n > O((\rho s + \sigma/\tau)^2\log p)$ under random designs. In addition, we relate the RDD condition to the irrepresentable condition, and highlight limitations of $SIS$.

High-dimensional Ordinary Least-squares Projection for Screening Variables

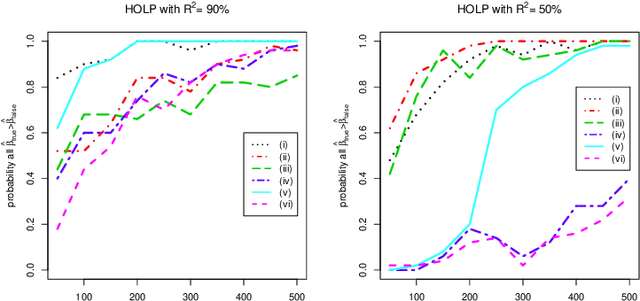
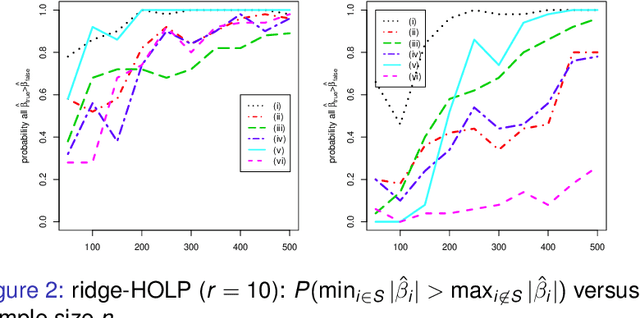
Variable selection is a challenging issue in statistical applications when the number of predictors $p$ far exceeds the number of observations $n$. In this ultra-high dimensional setting, the sure independence screening (SIS) procedure was introduced to significantly reduce the dimensionality by preserving the true model with overwhelming probability, before a refined second stage analysis. However, the aforementioned sure screening property strongly relies on the assumption that the important variables in the model have large marginal correlations with the response, which rarely holds in reality. To overcome this, we propose a novel and simple screening technique called the high-dimensional ordinary least-squares projection (HOLP). We show that HOLP possesses the sure screening property and gives consistent variable selection without the strong correlation assumption, and has a low computational complexity. A ridge type HOLP procedure is also discussed. Simulation study shows that HOLP performs competitively compared to many other marginal correlation based methods. An application to a mammalian eye disease data illustrates the attractiveness of HOLP.

Gradient-based kernel dimension reduction for supervised learning

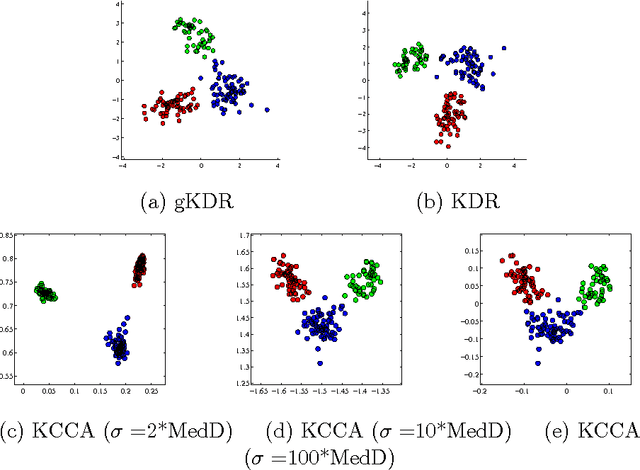
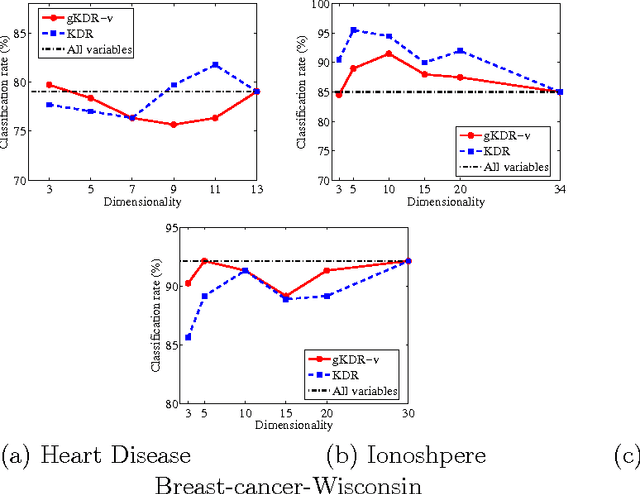
This paper proposes a novel kernel approach to linear dimension reduction for supervised learning. The purpose of the dimension reduction is to find directions in the input space to explain the output as effectively as possible. The proposed method uses an estimator for the gradient of regression function, based on the covariance operators on reproducing kernel Hilbert spaces. In comparison with other existing methods, the proposed one has wide applicability without strong assumptions on the distributions or the type of variables, and uses computationally simple eigendecomposition. Experimental results show that the proposed method successfully finds the effective directions with efficient computation.

Variational approximation for heteroscedastic linear models and matching pursuit algorithms

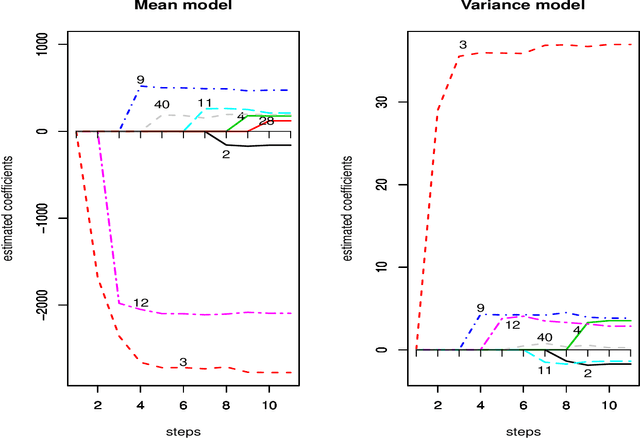
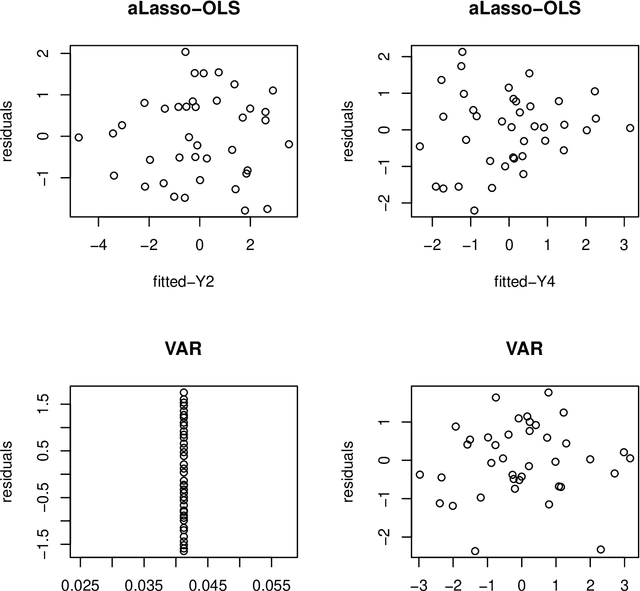
Modern statistical applications involving large data sets have focused attention on statistical methodologies which are both efficient computationally and able to deal with the screening of large numbers of different candidate models. Here we consider computationally efficient variational Bayes approaches to inference in high-dimensional heteroscedastic linear regression, where both the mean and variance are described in terms of linear functions of the predictors and where the number of predictors can be larger than the sample size. We derive a closed form variational lower bound on the log marginal likelihood useful for model selection, and propose a novel fast greedy search algorithm on the model space which makes use of one step optimization updates to the variational lower bound in the current model for screening large numbers of candidate predictor variables for inclusion/exclusion in a computationally thrifty way. We show that the model search strategy we suggest is related to widely used orthogonal matching pursuit algorithms for model search but yields a framework for potentially extending these algorithms to more complex models. The methodology is applied in simulations and in two real examples involving prediction for food constituents using NIR technology and prediction of disease progression in diabetes.