Gradient-based kernel dimension reduction for supervised learning
Paper and Code
Sep 02, 2011
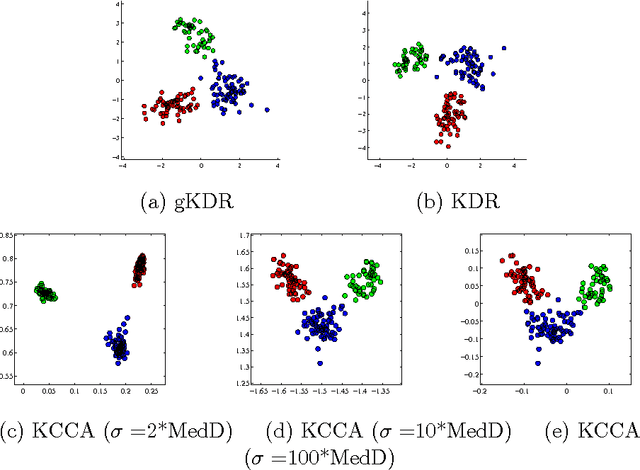

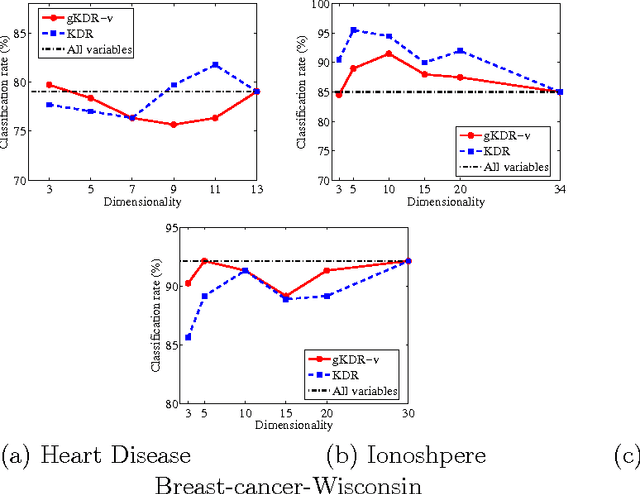
This paper proposes a novel kernel approach to linear dimension reduction for supervised learning. The purpose of the dimension reduction is to find directions in the input space to explain the output as effectively as possible. The proposed method uses an estimator for the gradient of regression function, based on the covariance operators on reproducing kernel Hilbert spaces. In comparison with other existing methods, the proposed one has wide applicability without strong assumptions on the distributions or the type of variables, and uses computationally simple eigendecomposition. Experimental results show that the proposed method successfully finds the effective directions with efficient computation.
* 21 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge