Variational approximation for heteroscedastic linear models and matching pursuit algorithms
Paper and Code
Mar 02, 2011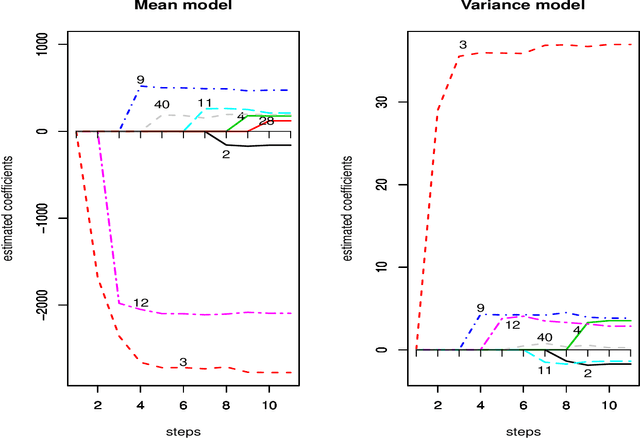

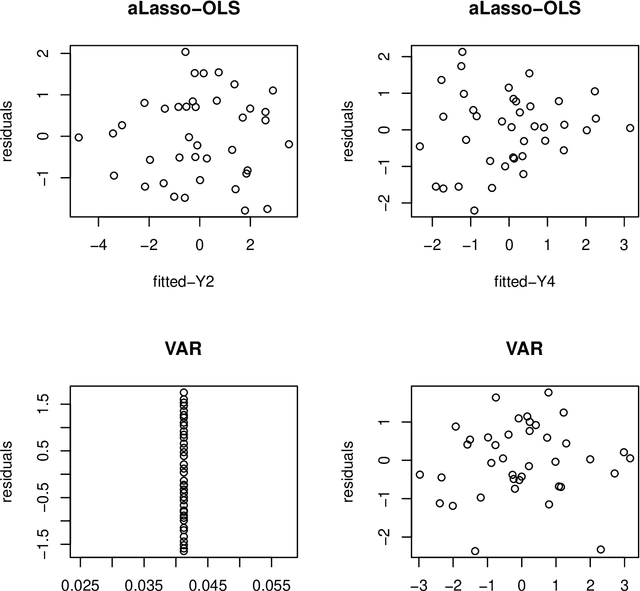

Modern statistical applications involving large data sets have focused attention on statistical methodologies which are both efficient computationally and able to deal with the screening of large numbers of different candidate models. Here we consider computationally efficient variational Bayes approaches to inference in high-dimensional heteroscedastic linear regression, where both the mean and variance are described in terms of linear functions of the predictors and where the number of predictors can be larger than the sample size. We derive a closed form variational lower bound on the log marginal likelihood useful for model selection, and propose a novel fast greedy search algorithm on the model space which makes use of one step optimization updates to the variational lower bound in the current model for screening large numbers of candidate predictor variables for inclusion/exclusion in a computationally thrifty way. We show that the model search strategy we suggest is related to widely used orthogonal matching pursuit algorithms for model search but yields a framework for potentially extending these algorithms to more complex models. The methodology is applied in simulations and in two real examples involving prediction for food constituents using NIR technology and prediction of disease progression in diabetes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge