Dominique Zosso
Consistency of archetypal analysis
Oct 19, 2020
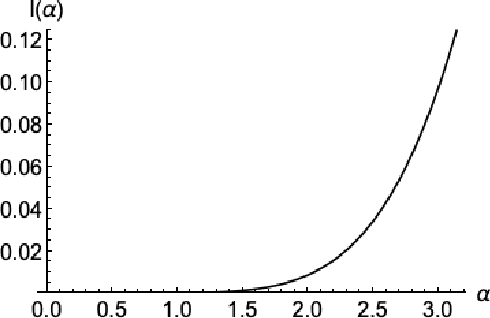
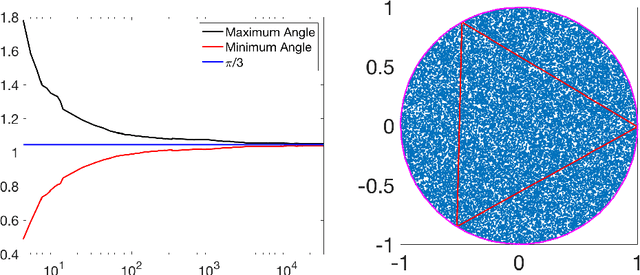
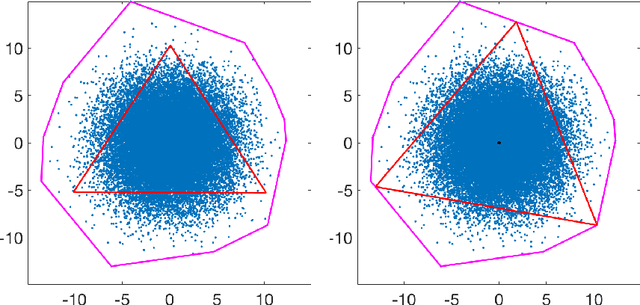
Abstract:Archetypal analysis is an unsupervised learning method that uses a convex polytope to summarize multivariate data. For fixed $k$, the method finds a convex polytope with $k$ vertices, called archetype points, such that the polytope is contained in the convex hull of the data and the mean squared distance between the data and the polytope is minimal. In this paper, we prove a consistency result that shows if the data is independently sampled from a probability measure with bounded support, then the archetype points converge to a solution of the continuum version of the problem, of which we identify and establish several properties. We also obtain the convergence rate of the optimal objective values under appropriate assumptions on the distribution. If the data is independently sampled from a distribution with unbounded support, we also prove a consistency result for a modified method that penalizes the dispersion of the archetype points. Our analysis is supported by detailed computational experiments of the archetype points for data sampled from the uniform distribution in a disk, the normal distribution, an annular distribution, and a Gaussian mixture model.
Unsupervised Classification in Hyperspectral Imagery with Nonlocal Total Variation and Primal-Dual Hybrid Gradient Algorithm
Feb 13, 2017
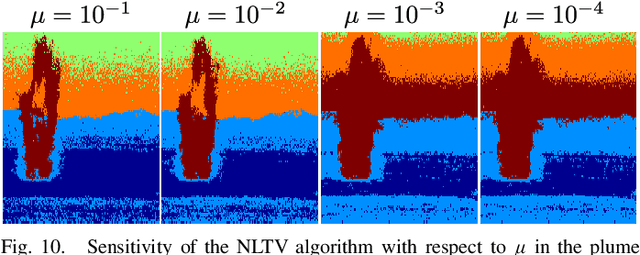


Abstract:In this paper, a graph-based nonlocal total variation method (NLTV) is proposed for unsupervised classification of hyperspectral images (HSI). The variational problem is solved by the primal-dual hybrid gradient (PDHG) algorithm. By squaring the labeling function and using a stable simplex clustering routine, an unsupervised clustering method with random initialization can be implemented. The effectiveness of this proposed algorithm is illustrated on both synthetic and real-world HSI, and numerical results show that the proposed algorithm outperforms other standard unsupervised clustering methods such as spherical K-means, nonnegative matrix factorization (NMF), and the graph-based Merriman-Bence-Osher (MBO) scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge