Vision Transformer Pruning Via Matrix Decomposition

This is a further development of Vision Transformer Pruning via matrix decomposition. The purpose of the Vision Transformer Pruning is to prune the dimension of the linear projection of the dataset by learning their associated importance score in order to reduce the storage, run-time memory, and computational demands. In this paper we further reduce dimension and complexity of the linear projection by implementing and comparing several matrix decomposition methods while preserving the generated important features. We end up selected the Singular Value Decomposition as the method to achieve our goal by comparing the original accuracy scores in the original Github repository and the accuracy scores of using those matrix decomposition methods, including Singular Value Decomposition, four versions of QR Decomposition, and LU factorization.

Topological Interpretations of GPT-3

This is an experiential study of investigating a consistent method for deriving the correlation between sentence vector and semantic meaning of a sentence. We first used three state-of-the-art word/sentence embedding methods including GPT-3, Word2Vec, and Sentence-BERT, to embed plain text sentence strings into high dimensional spaces. Then we compute the pairwise distance between any possible combination of two sentence vectors in an embedding space and map them into a matrix. Based on each distance matrix, we compute the correlation of distances of a sentence vector with respect to the other sentence vectors in an embedding space. Then we compute the correlation of each pair of the distance matrices. We observed correlations of the same sentence in different embedding spaces and correlations of different sentences in the same embedding space. These observations are consistent with our hypothesis and take us to the next stage.

P-tensors: a General Formalism for Constructing Higher Order Message Passing Networks

Several recent papers have recently shown that higher order graph neural networks can achieve better accuracy than their standard message passing counterparts, especially on highly structured graphs such as molecules. These models typically work by considering higher order representations of subgraphs contained within a given graph and then perform some linear maps between them. We formalize these structures as permutation equivariant tensors, or P-tensors, and derive a basis for all linear maps between arbitrary order equivariant P-tensors. Experimentally, we demonstrate this paradigm achieves state of the art performance on several benchmark datasets.

Clustering US Counties to Find Patterns Related to the COVID-19 Pandemic

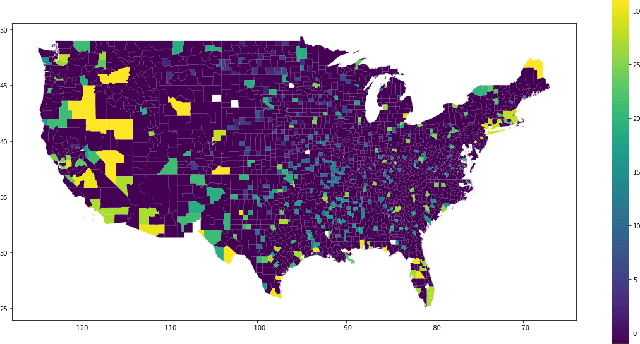
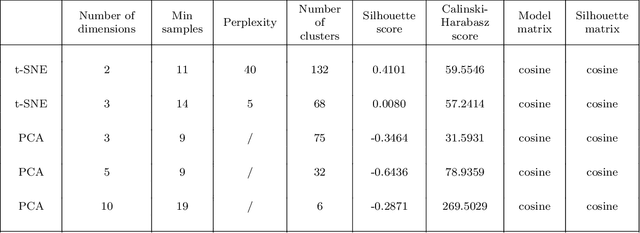
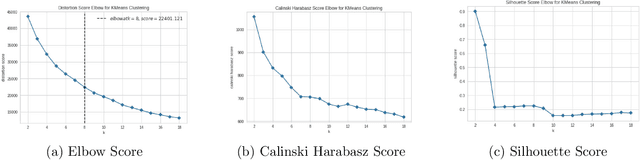
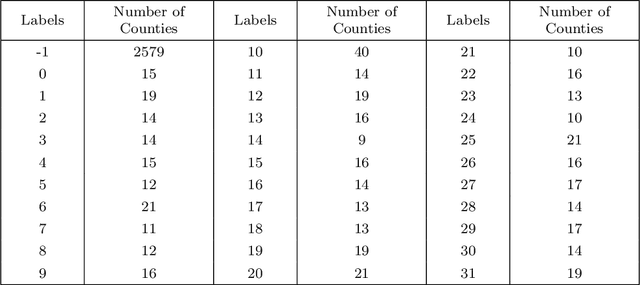
When COVID-19 first started spreading and quarantine was implemented, the Society for Industrial and Applied Mathematics (SIAM) Student Chapter at the University of Minnesota-Twin Cities began a collaboration with Ecolab to use our skills as data scientists and mathematicians to extract useful insights from relevant data relating to the pandemic. This collaboration consisted of multiple groups working on different projects. In this write-up we focus on using clustering techniques to help us find groups of similar counties in the US and use that to help us understand the pandemic. Our team for this project consisted of University of Minnesota students Cora Brown, Sarah Milstein, Tianyi Sun, and Cooper Zhao, with help from Ecolab Data Scientist Jimmy Broomfield and University of Minnesota student Skye Ke. In the sections below we describe all of the work done for this project. In Section 2, we list the data we gathered, as well as the feature engineering we performed. In Section 3, we describe the metrics we used for evaluating our models. In Section 4, we explain the methods we used for interpreting the results of our various clustering approaches. In Section 5, we describe the different clustering methods we implemented. In Section 6, we present the results of our clustering techniques and provide relevant interpretation. Finally, in Section 7, we provide some concluding remarks comparing the different clustering methods.