Equivariant Polynomial Functional Networks
Paper and Code
Oct 05, 2024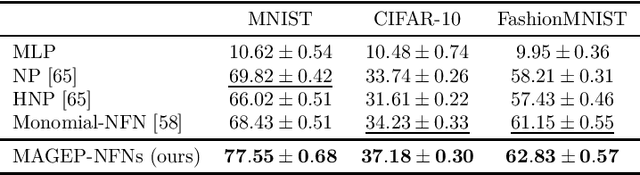



Neural Functional Networks (NFNs) have gained increasing interest due to their wide range of applications, including extracting information from implicit representations of data, editing network weights, and evaluating policies. A key design principle of NFNs is their adherence to the permutation and scaling symmetries inherent in the connectionist structure of the input neural networks. Recent NFNs have been proposed with permutation and scaling equivariance based on either graph-based message-passing mechanisms or parameter-sharing mechanisms. However, graph-based equivariant NFNs suffer from high memory consumption and long running times. On the other hand, parameter-sharing-based NFNs built upon equivariant linear layers exhibit lower memory consumption and faster running time, yet their expressivity is limited due to the large size of the symmetric group of the input neural networks. The challenge of designing a permutation and scaling equivariant NFN that maintains low memory consumption and running time while preserving expressivity remains unresolved. In this paper, we propose a novel solution with the development of MAGEP-NFN (Monomial mAtrix Group Equivariant Polynomial NFN). Our approach follows the parameter-sharing mechanism but differs from previous works by constructing a nonlinear equivariant layer represented as a polynomial in the input weights. This polynomial formulation enables us to incorporate additional relationships between weights from different input hidden layers, enhancing the model's expressivity while keeping memory consumption and running time low, thereby addressing the aforementioned challenge. We provide empirical evidence demonstrating that MAGEP-NFN achieves competitive performance and efficiency compared to existing baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge