Adaptive Prompting for Continual Relation Extraction: A Within-Task Variance Perspective

To address catastrophic forgetting in Continual Relation Extraction (CRE), many current approaches rely on memory buffers to rehearse previously learned knowledge while acquiring new tasks. Recently, prompt-based methods have emerged as potent alternatives to rehearsal-based strategies, demonstrating strong empirical performance. However, upon analyzing existing prompt-based approaches for CRE, we identified several critical limitations, such as inaccurate prompt selection, inadequate mechanisms for mitigating forgetting in shared parameters, and suboptimal handling of cross-task and within-task variances. To overcome these challenges, we draw inspiration from the relationship between prefix-tuning and mixture of experts, proposing a novel approach that employs a prompt pool for each task, capturing variations within each task while enhancing cross-task variances. Furthermore, we incorporate a generative model to consolidate prior knowledge within shared parameters, eliminating the need for explicit data storage. Extensive experiments validate the efficacy of our approach, demonstrating superior performance over state-of-the-art prompt-based and rehearsal-free methods in continual relation extraction.

Equivariant Polynomial Functional Networks

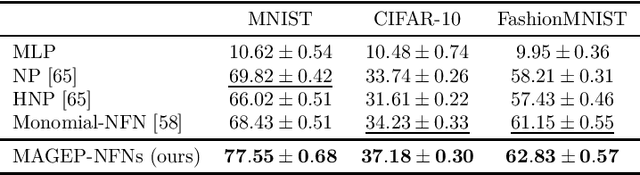
Neural Functional Networks (NFNs) have gained increasing interest due to their wide range of applications, including extracting information from implicit representations of data, editing network weights, and evaluating policies. A key design principle of NFNs is their adherence to the permutation and scaling symmetries inherent in the connectionist structure of the input neural networks. Recent NFNs have been proposed with permutation and scaling equivariance based on either graph-based message-passing mechanisms or parameter-sharing mechanisms. However, graph-based equivariant NFNs suffer from high memory consumption and long running times. On the other hand, parameter-sharing-based NFNs built upon equivariant linear layers exhibit lower memory consumption and faster running time, yet their expressivity is limited due to the large size of the symmetric group of the input neural networks. The challenge of designing a permutation and scaling equivariant NFN that maintains low memory consumption and running time while preserving expressivity remains unresolved. In this paper, we propose a novel solution with the development of MAGEP-NFN (Monomial mAtrix Group Equivariant Polynomial NFN). Our approach follows the parameter-sharing mechanism but differs from previous works by constructing a nonlinear equivariant layer represented as a polynomial in the input weights. This polynomial formulation enables us to incorporate additional relationships between weights from different input hidden layers, enhancing the model's expressivity while keeping memory consumption and running time low, thereby addressing the aforementioned challenge. We provide empirical evidence demonstrating that MAGEP-NFN achieves competitive performance and efficiency compared to existing baselines.

Equivariant Neural Functional Networks for Transformers

This paper systematically explores neural functional networks (NFN) for transformer architectures. NFN are specialized neural networks that treat the weights, gradients, or sparsity patterns of a deep neural network (DNN) as input data and have proven valuable for tasks such as learnable optimizers, implicit data representations, and weight editing. While NFN have been extensively developed for MLP and CNN, no prior work has addressed their design for transformers, despite the importance of transformers in modern deep learning. This paper aims to address this gap by providing a systematic study of NFN for transformers. We first determine the maximal symmetric group of the weights in a multi-head attention module as well as a necessary and sufficient condition under which two sets of hyperparameters of the multi-head attention module define the same function. We then define the weight space of transformer architectures and its associated group action, which leads to the design principles for NFN in transformers. Based on these, we introduce Transformer-NFN, an NFN that is equivariant under this group action. Additionally, we release a dataset of more than 125,000 Transformers model checkpoints trained on two datasets with two different tasks, providing a benchmark for evaluating Transformer-NFN and encouraging further research on transformer training and performance.