Revisiting Kernel Attention with Correlated Gaussian Process Representation

Transformers have increasingly become the de facto method to model sequential data with state-of-the-art performance. Due to its widespread use, being able to estimate and calibrate its modeling uncertainty is important to understand and design robust transformer models. To achieve this, previous works have used Gaussian processes (GPs) to perform uncertainty calibration for the attention units of transformers and attained notable successes. However, such approaches have to confine the transformers to the space of symmetric attention to ensure the necessary symmetric requirement of their GP's kernel specification, which reduces the representation capacity of the model. To mitigate this restriction, we propose the Correlated Gaussian Process Transformer (CGPT), a new class of transformers whose self-attention units are modeled as cross-covariance between two correlated GPs (CGPs). This allows asymmetries in attention and can enhance the representation capacity of GP-based transformers. We also derive a sparse approximation for CGP to make it scale better. Our empirical studies show that both CGP-based and sparse CGP-based transformers achieve better performance than state-of-the-art GP-based transformers on a variety of benchmark tasks. The code for our experiments is available at https://github.com/MinhLong210/CGP-Transformers.

A Clifford Algebraic Approach to E(n)-Equivariant High-order Graph Neural Networks

Designing neural network architectures that can handle data symmetry is crucial. This is especially important for geometric graphs whose properties are equivariance under Euclidean transformations. Current equivariant graph neural networks (EGNNs), particularly those using message passing, have a limitation in expressive power. Recent high-order graph neural networks can overcome this limitation, yet they lack equivariance properties, representing a notable drawback in certain applications in chemistry and physical sciences. In this paper, we introduce the Clifford Group Equivariant Graph Neural Networks (CG-EGNNs), a novel EGNN that enhances high-order message passing by integrating high-order local structures in the context of Clifford algebras. As a key benefit of using Clifford algebras, CG-EGNN can learn functions that capture equivariance from positional features. By adopting the high-order message passing mechanism, CG-EGNN gains richer information from neighbors, thus improving model performance. Furthermore, we establish the universality property of the $k$-hop message passing framework, showcasing greater expressive power of CG-EGNNs with additional $k$-hop message passing mechanism. We empirically validate that CG-EGNNs outperform previous methods on various benchmarks including n-body, CMU motion capture, and MD17, highlighting their effectiveness in geometric deep learning.

Equivariant Polynomial Functional Networks

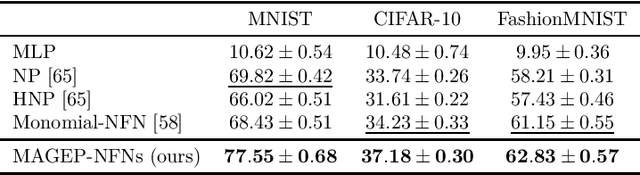
Neural Functional Networks (NFNs) have gained increasing interest due to their wide range of applications, including extracting information from implicit representations of data, editing network weights, and evaluating policies. A key design principle of NFNs is their adherence to the permutation and scaling symmetries inherent in the connectionist structure of the input neural networks. Recent NFNs have been proposed with permutation and scaling equivariance based on either graph-based message-passing mechanisms or parameter-sharing mechanisms. However, graph-based equivariant NFNs suffer from high memory consumption and long running times. On the other hand, parameter-sharing-based NFNs built upon equivariant linear layers exhibit lower memory consumption and faster running time, yet their expressivity is limited due to the large size of the symmetric group of the input neural networks. The challenge of designing a permutation and scaling equivariant NFN that maintains low memory consumption and running time while preserving expressivity remains unresolved. In this paper, we propose a novel solution with the development of MAGEP-NFN (Monomial mAtrix Group Equivariant Polynomial NFN). Our approach follows the parameter-sharing mechanism but differs from previous works by constructing a nonlinear equivariant layer represented as a polynomial in the input weights. This polynomial formulation enables us to incorporate additional relationships between weights from different input hidden layers, enhancing the model's expressivity while keeping memory consumption and running time low, thereby addressing the aforementioned challenge. We provide empirical evidence demonstrating that MAGEP-NFN achieves competitive performance and efficiency compared to existing baselines.

Equivariant Neural Functional Networks for Transformers

This paper systematically explores neural functional networks (NFN) for transformer architectures. NFN are specialized neural networks that treat the weights, gradients, or sparsity patterns of a deep neural network (DNN) as input data and have proven valuable for tasks such as learnable optimizers, implicit data representations, and weight editing. While NFN have been extensively developed for MLP and CNN, no prior work has addressed their design for transformers, despite the importance of transformers in modern deep learning. This paper aims to address this gap by providing a systematic study of NFN for transformers. We first determine the maximal symmetric group of the weights in a multi-head attention module as well as a necessary and sufficient condition under which two sets of hyperparameters of the multi-head attention module define the same function. We then define the weight space of transformer architectures and its associated group action, which leads to the design principles for NFN in transformers. Based on these, we introduce Transformer-NFN, an NFN that is equivariant under this group action. Additionally, we release a dataset of more than 125,000 Transformers model checkpoints trained on two datasets with two different tasks, providing a benchmark for evaluating Transformer-NFN and encouraging further research on transformer training and performance.