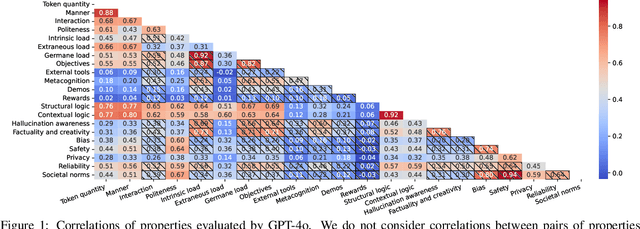
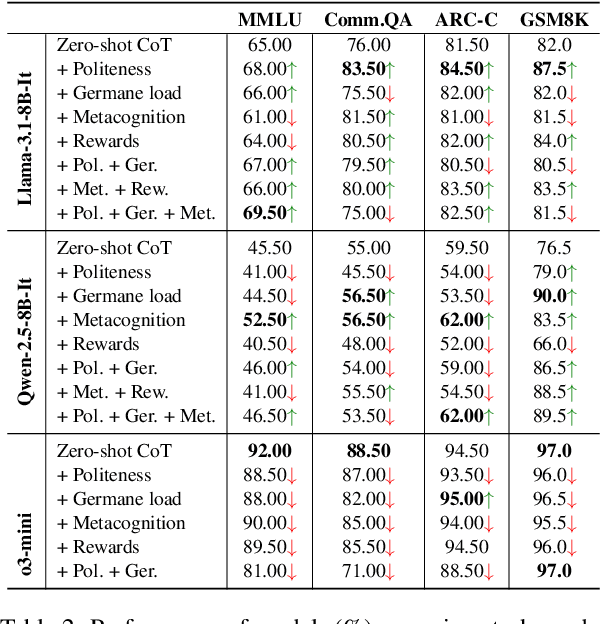
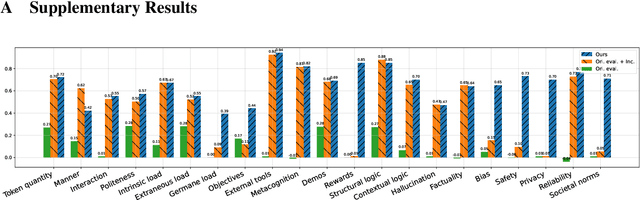
What Makes a Good Natural Language Prompt?

As large language models (LLMs) have progressed towards more human-like and human--AI communications have become prevalent, prompting has emerged as a decisive component. However, there is limited conceptual consensus on what exactly quantifies natural language prompts. We attempt to address this question by conducting a meta-analysis surveying more than 150 prompting-related papers from leading NLP and AI conferences from 2022 to 2025 and blogs. We propose a property- and human-centric framework for evaluating prompt quality, encompassing 21 properties categorized into six dimensions. We then examine how existing studies assess their impact on LLMs, revealing their imbalanced support across models and tasks, and substantial research gaps. Further, we analyze correlations among properties in high-quality natural language prompts, deriving prompting recommendations. We then empirically explore multi-property prompt enhancements in reasoning tasks, observing that single-property enhancements often have the greatest impact. Finally, we discover that instruction-tuning on property-enhanced prompts can result in better reasoning models. Our findings establish a foundation for property-centric prompt evaluation and optimization, bridging the gaps between human--AI communication and opening new prompting research directions.

Revisiting Kernel Attention with Correlated Gaussian Process Representation

Transformers have increasingly become the de facto method to model sequential data with state-of-the-art performance. Due to its widespread use, being able to estimate and calibrate its modeling uncertainty is important to understand and design robust transformer models. To achieve this, previous works have used Gaussian processes (GPs) to perform uncertainty calibration for the attention units of transformers and attained notable successes. However, such approaches have to confine the transformers to the space of symmetric attention to ensure the necessary symmetric requirement of their GP's kernel specification, which reduces the representation capacity of the model. To mitigate this restriction, we propose the Correlated Gaussian Process Transformer (CGPT), a new class of transformers whose self-attention units are modeled as cross-covariance between two correlated GPs (CGPs). This allows asymmetries in attention and can enhance the representation capacity of GP-based transformers. We also derive a sparse approximation for CGP to make it scale better. Our empirical studies show that both CGP-based and sparse CGP-based transformers achieve better performance than state-of-the-art GP-based transformers on a variety of benchmark tasks. The code for our experiments is available at https://github.com/MinhLong210/CGP-Transformers.

Improving Generative Flow Networks with Path Regularization

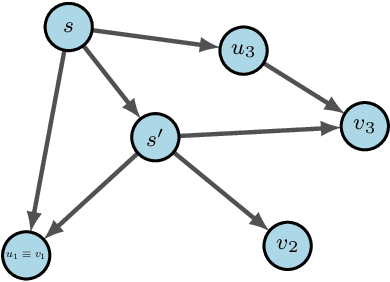
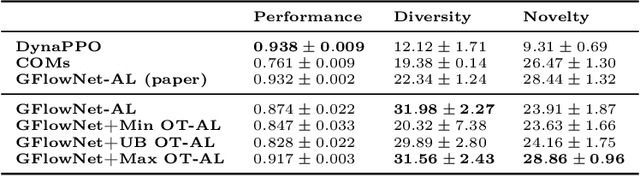
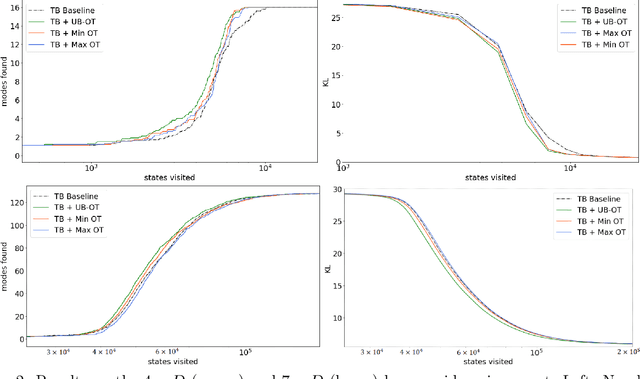
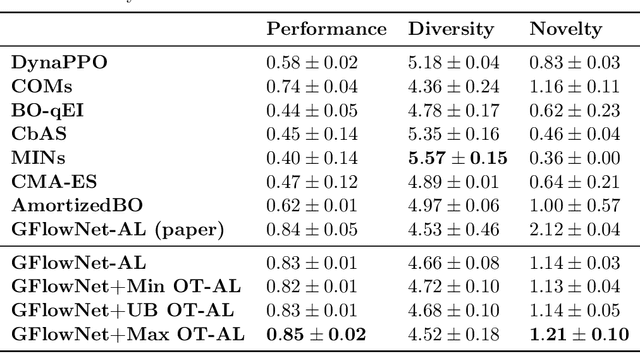
Generative Flow Networks (GFlowNets) are recently proposed models for learning stochastic policies that generate compositional objects by sequences of actions with the probability proportional to a given reward function. The central problem of GFlowNets is to improve their exploration and generalization. In this work, we propose a novel path regularization method based on optimal transport theory that places prior constraints on the underlying structure of the GFlowNets. The prior is designed to help the GFlowNets better discover the latent structure of the target distribution or enhance its ability to explore the environment in the context of active learning. The path regularization controls the flow in GFlowNets to generate more diverse and novel candidates via maximizing the optimal transport distances between two forward policies or to improve the generalization via minimizing the optimal transport distances. In addition, we derive an efficient implementation of the regularization by finding its closed form solutions in specific cases and a meaningful upper bound that can be used as an approximation to minimize the regularization term. We empirically demonstrate the advantage of our path regularization on a wide range of tasks, including synthetic hypergrid environment modeling, discrete probabilistic modeling, and biological sequence design.