Detecting Omissions in Geographic Maps through Computer Vision

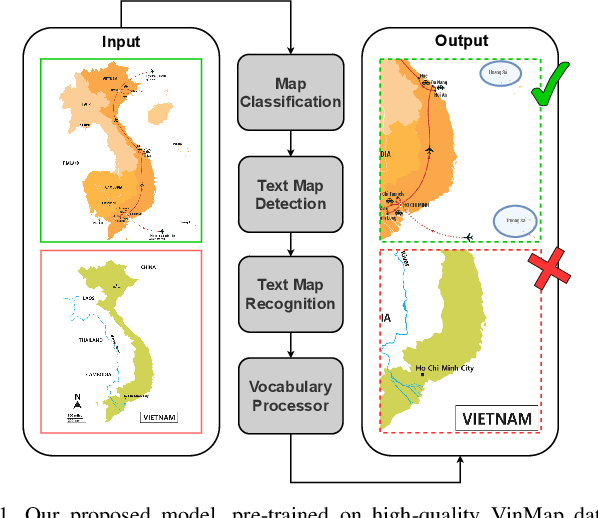
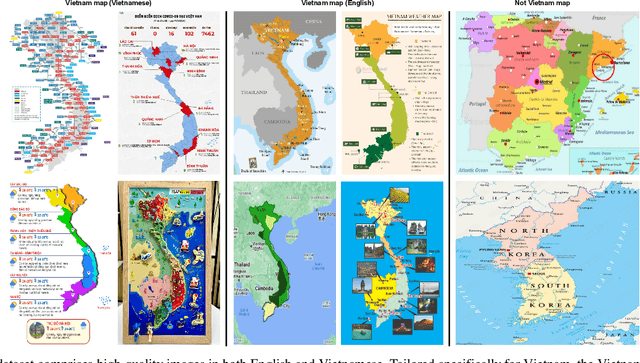
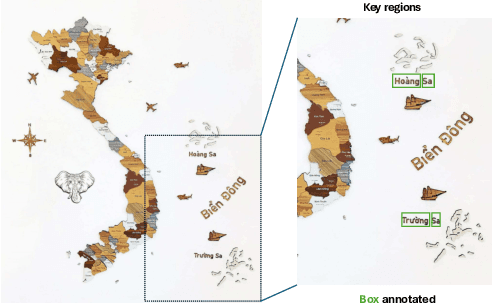
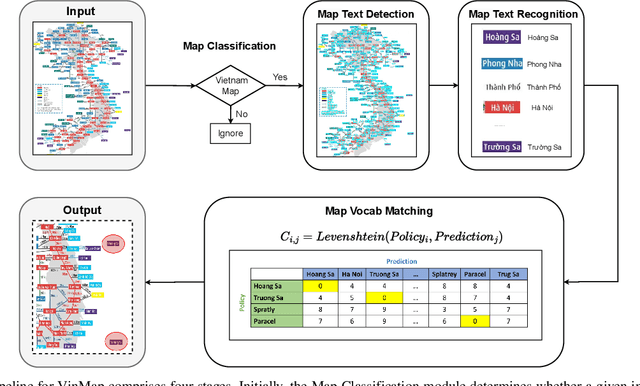
This paper explores the application of computer vision technologies to the analysis of maps, an area with substantial historical, cultural, and political significance. Our focus is on developing and evaluating a method for automatically identifying maps that depict specific regions and feature landmarks with designated names, a task that involves complex challenges due to the diverse styles and methods used in map creation. We address three main subtasks: differentiating maps from non-maps, verifying the accuracy of the region depicted, and confirming the presence or absence of particular landmark names through advanced text recognition techniques. Our approach utilizes a Convolutional Neural Network and transfer learning to differentiate maps from non-maps, verify the accuracy of depicted regions, and confirm landmark names through advanced text recognition. We also introduce the VinMap dataset, containing annotated map images of Vietnam, to train and test our method. Experiments on this dataset demonstrate that our technique achieves F1-score of 85.51% for identifying maps excluding specific territorial landmarks. This result suggests practical utility and indicates areas for future improvement.

Improving Generative Flow Networks with Path Regularization

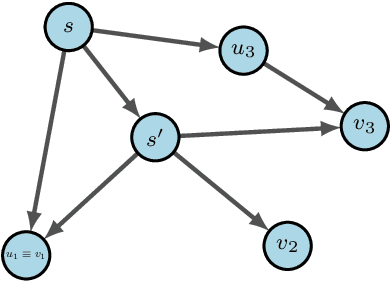
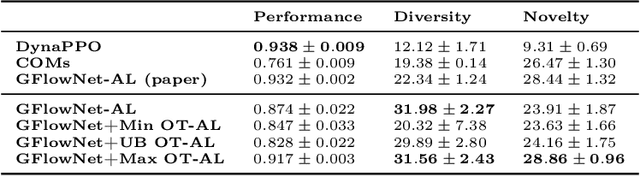
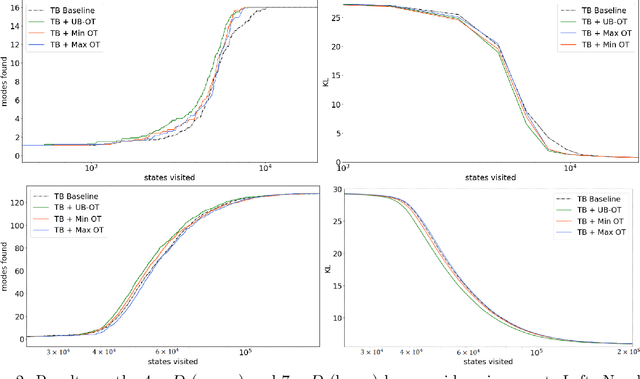
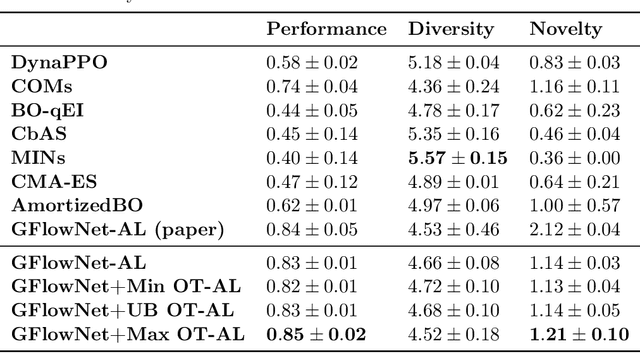
Generative Flow Networks (GFlowNets) are recently proposed models for learning stochastic policies that generate compositional objects by sequences of actions with the probability proportional to a given reward function. The central problem of GFlowNets is to improve their exploration and generalization. In this work, we propose a novel path regularization method based on optimal transport theory that places prior constraints on the underlying structure of the GFlowNets. The prior is designed to help the GFlowNets better discover the latent structure of the target distribution or enhance its ability to explore the environment in the context of active learning. The path regularization controls the flow in GFlowNets to generate more diverse and novel candidates via maximizing the optimal transport distances between two forward policies or to improve the generalization via minimizing the optimal transport distances. In addition, we derive an efficient implementation of the regularization by finding its closed form solutions in specific cases and a meaningful upper bound that can be used as an approximation to minimize the regularization term. We empirically demonstrate the advantage of our path regularization on a wide range of tasks, including synthetic hypergrid environment modeling, discrete probabilistic modeling, and biological sequence design.