Bayes Optimal Algorithm is Suboptimal in Frequentist Best Arm Identification
Paper and Code
Feb 10, 2022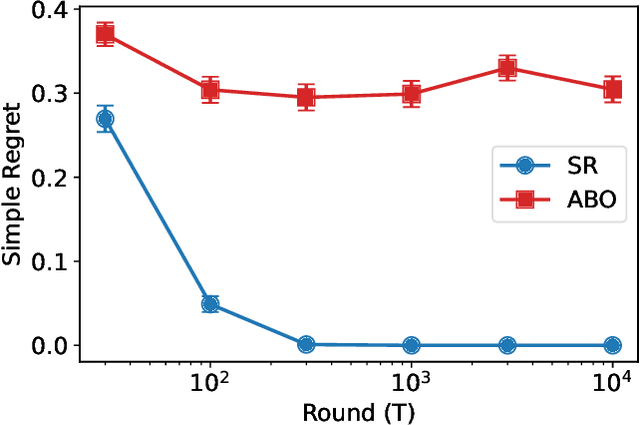
We consider the fixed-budget best arm identification problem with Normal rewards. In this problem, the forecaster is given $K$ arms (treatments) and $T$ time steps. The forecaster attempts to find the best arm in terms of the largest mean via an adaptive experiment conducted with an algorithm. The performance of the algorithm is measured by the simple regret, or the quality of the estimated best arm. It is known that the frequentist simple regret can be exponentially small to $T$ for any fixed parameters, whereas the Bayesian simple regret is $\Theta(T^{-1})$ over a continuous prior distribution. This paper shows that Bayes optimal algorithm, which minimizes the Bayesian simple regret, does not have an exponential simple regret for some parameters. This finding contrasts with the many results indicating the asymptotic equivalence of Bayesian and frequentist algorithms in fixed sampling regimes. While the Bayes optimal algorithm is described in terms of a recursive equation that is virtually impossible to compute exactly, we pave the way to an analysis by introducing a key quantity that we call the expected Bellman improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge