Optimal Algorithms for Private Online Learning in a Stochastic Environment
Paper and Code
Feb 16, 2021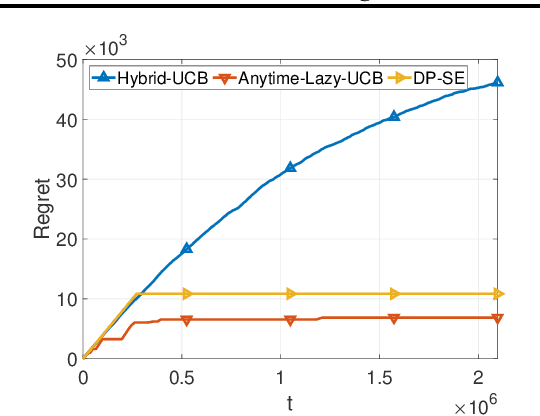
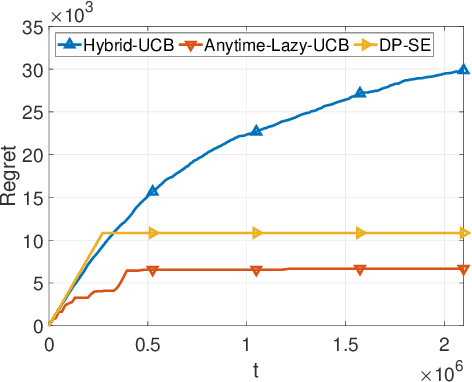
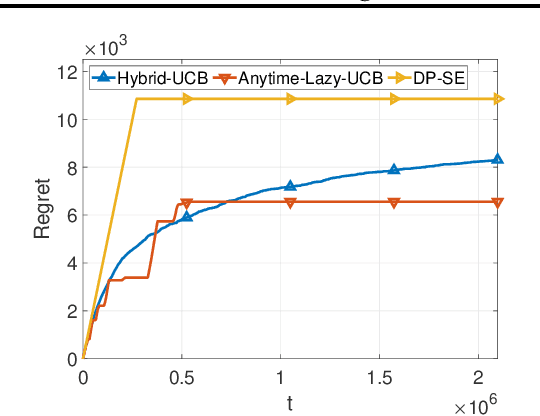
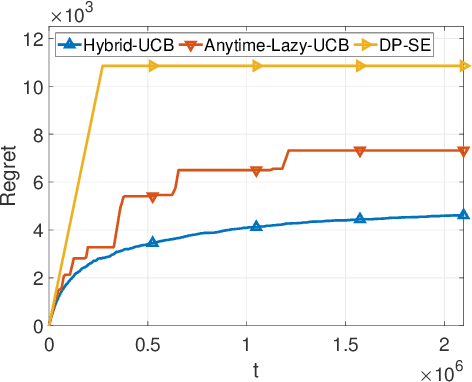
We consider two variants of private stochastic online learning. The first variant is differentially private stochastic bandits. Previously, Sajed and Sheffet (2019) devised the DP Successive Elimination (DP-SE) algorithm that achieves the optimal $ O \biggl(\sum\limits_{1\le j \le K: \Delta_j >0} \frac{ \log T}{ \Delta_j} + \frac{ K\log T}{\epsilon} \biggr)$ problem-dependent regret bound, where $K$ is the number of arms, $\Delta_j$ is the mean reward gap of arm $j$, $T$ is the time horizon, and $\epsilon$ is the required privacy parameter. However, like other elimination style algorithms, it is not an anytime algorithm. Until now, it was not known whether UCB-based algorithms could achieve this optimal regret bound. We present an anytime, UCB-based algorithm that achieves optimality. Our experiments show that the UCB-based algorithm is competitive with DP-SE. The second variant is the full information version of private stochastic online learning. Specifically, for the problems of decision-theoretic online learning with stochastic rewards, we present the first algorithm that achieves an $ O \left( \frac{ \log K}{ \Delta_{\min}} + \frac{ \log K}{\epsilon} \right)$ regret bound, where $\Delta_{\min}$ is the minimum mean reward gap. The key idea behind our good theoretical guarantees in both settings is the forgetfulness, i.e., decisions are made based on a certain amount of newly obtained observations instead of all the observations obtained from the very beginning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge