Youming Tao
Second-Order Convergence in Private Stochastic Non-Convex Optimization
May 21, 2025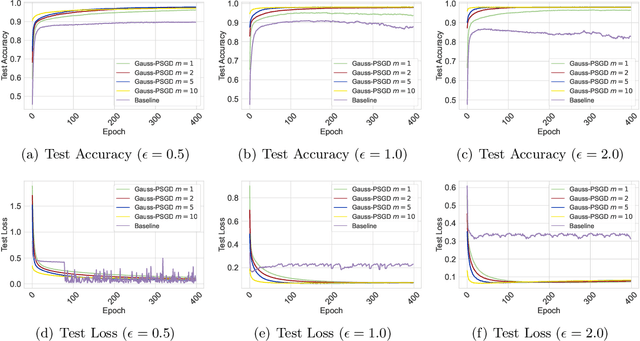
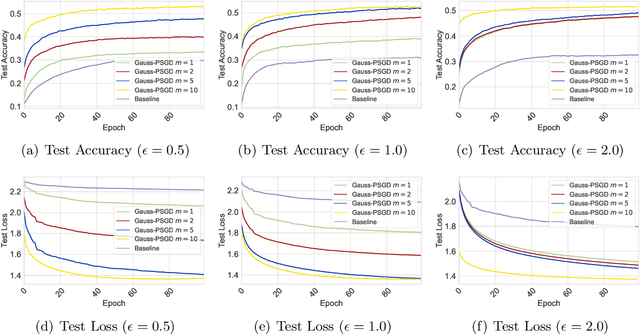
Abstract:We investigate the problem of finding second-order stationary points (SOSP) in differentially private (DP) stochastic non-convex optimization. Existing methods suffer from two key limitations: (i) inaccurate convergence error rate due to overlooking gradient variance in the saddle point escape analysis, and (ii) dependence on auxiliary private model selection procedures for identifying DP-SOSP, which can significantly impair utility, particularly in distributed settings. To address these issues, we propose a generic perturbed stochastic gradient descent (PSGD) framework built upon Gaussian noise injection and general gradient oracles. A core innovation of our framework is using model drift distance to determine whether PSGD escapes saddle points, ensuring convergence to approximate local minima without relying on second-order information or additional DP-SOSP identification. By leveraging the adaptive DP-SPIDER estimator as a specific gradient oracle, we develop a new DP algorithm that rectifies the convergence error rates reported in prior work. We further extend this algorithm to distributed learning with arbitrarily heterogeneous data, providing the first formal guarantees for finding DP-SOSP in such settings. Our analysis also highlights the detrimental impacts of private selection procedures in distributed learning under high-dimensional models, underscoring the practical benefits of our design. Numerical experiments on real-world datasets validate the efficacy of our approach.
Communication Efficient and Provable Federated Unlearning
Jan 19, 2024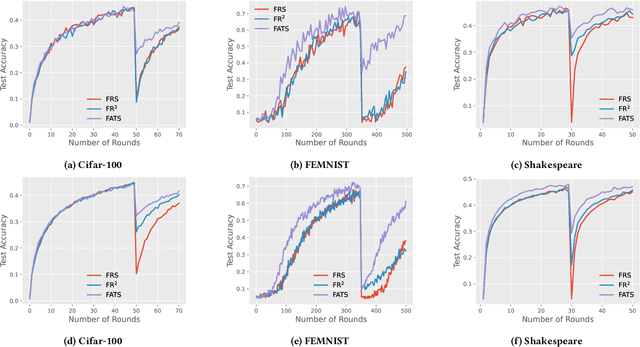
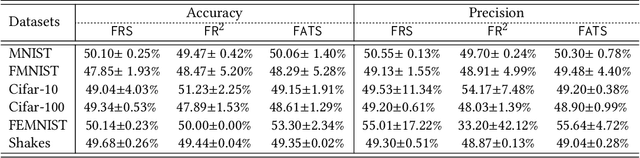
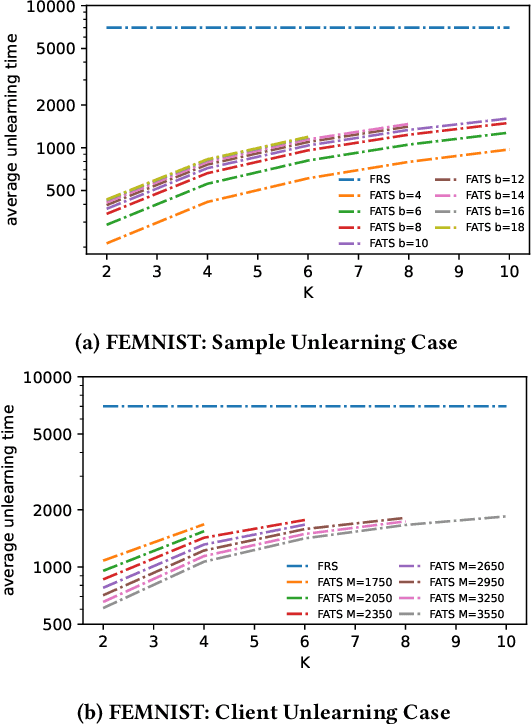

Abstract:We study federated unlearning, a novel problem to eliminate the impact of specific clients or data points on the global model learned via federated learning (FL). This problem is driven by the right to be forgotten and the privacy challenges in FL. We introduce a new framework for exact federated unlearning that meets two essential criteria: \textit{communication efficiency} and \textit{exact unlearning provability}. To our knowledge, this is the first work to tackle both aspects coherently. We start by giving a rigorous definition of \textit{exact} federated unlearning, which guarantees that the unlearned model is statistically indistinguishable from the one trained without the deleted data. We then pinpoint the key property that enables fast exact federated unlearning: total variation (TV) stability, which measures the sensitivity of the model parameters to slight changes in the dataset. Leveraging this insight, we develop a TV-stable FL algorithm called \texttt{FATS}, which modifies the classical \texttt{\underline{F}ed\underline{A}vg} algorithm for \underline{T}V \underline{S}tability and employs local SGD with periodic averaging to lower the communication round. We also design efficient unlearning algorithms for \texttt{FATS} under two settings: client-level and sample-level unlearning. We provide theoretical guarantees for our learning and unlearning algorithms, proving that they achieve exact federated unlearning with reasonable convergence rates for both the original and unlearned models. We empirically validate our framework on 6 benchmark datasets, and show its superiority over state-of-the-art methods in terms of accuracy, communication cost, computation cost, and unlearning efficacy.
Resource-Adaptive Newton's Method for Distributed Learning
Sep 02, 2023Abstract:Distributed stochastic optimization methods based on Newton's method offer significant advantages over first-order methods by leveraging curvature information for improved performance. However, the practical applicability of Newton's method is hindered in large-scale and heterogeneous learning environments due to challenges such as high computation and communication costs associated with the Hessian matrix, sub-model diversity, staleness in training, and data heterogeneity. To address these challenges, this paper introduces a novel and efficient algorithm called RANL, which overcomes the limitations of Newton's method by employing a simple Hessian initialization and adaptive assignments of training regions. The algorithm demonstrates impressive convergence properties, which are rigorously analyzed under standard assumptions in stochastic optimization. The theoretical analysis establishes that RANL achieves a linear convergence rate while effectively adapting to available resources and maintaining high efficiency. Unlike traditional first-order methods, RANL exhibits remarkable independence from the condition number of the problem and eliminates the need for complex parameter tuning. These advantages make RANL a promising approach for distributed stochastic optimization in practical scenarios.
Byzantine-Resilient Federated Learning at Edge
Mar 18, 2023



Abstract:Both Byzantine resilience and communication efficiency have attracted tremendous attention recently for their significance in edge federated learning. However, most existing algorithms may fail when dealing with real-world irregular data that behaves in a heavy-tailed manner. To address this issue, we study the stochastic convex and non-convex optimization problem for federated learning at edge and show how to handle heavy-tailed data while retaining the Byzantine resilience, communication efficiency and the optimal statistical error rates simultaneously. Specifically, we first present a Byzantine-resilient distributed gradient descent algorithm that can handle the heavy-tailed data and meanwhile converge under the standard assumptions. To reduce the communication overhead, we further propose another algorithm that incorporates gradient compression techniques to save communication costs during the learning process. Theoretical analysis shows that our algorithms achieve order-optimal statistical error rate in presence of Byzantine devices. Finally, we conduct extensive experiments on both synthetic and real-world datasets to verify the efficacy of our algorithms.
On Private and Robust Bandits
Feb 06, 2023
Abstract:We study private and robust multi-armed bandits (MABs), where the agent receives Huber's contaminated heavy-tailed rewards and meanwhile needs to ensure differential privacy. We first present its minimax lower bound, characterizing the information-theoretic limit of regret with respect to privacy budget, contamination level and heavy-tailedness. Then, we propose a meta-algorithm that builds on a private and robust mean estimation sub-routine \texttt{PRM} that essentially relies on reward truncation and the Laplace mechanism only. For two different heavy-tailed settings, we give specific schemes of \texttt{PRM}, which enable us to achieve nearly-optimal regret. As by-products of our main results, we also give the first minimax lower bound for private heavy-tailed MABs (i.e., without contamination). Moreover, our two proposed truncation-based \texttt{PRM} achieve the optimal trade-off between estimation accuracy, privacy and robustness. Finally, we support our theoretical results with experimental studies.
Optimal Rates of (Locally) Differentially Private Heavy-tailed Multi-Armed Bandits
Jun 07, 2021
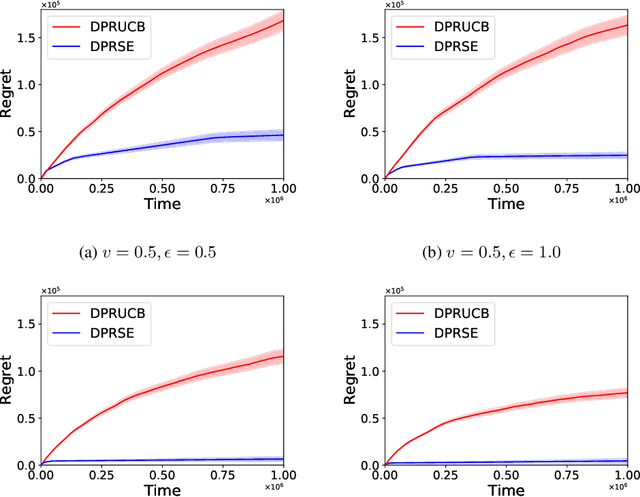
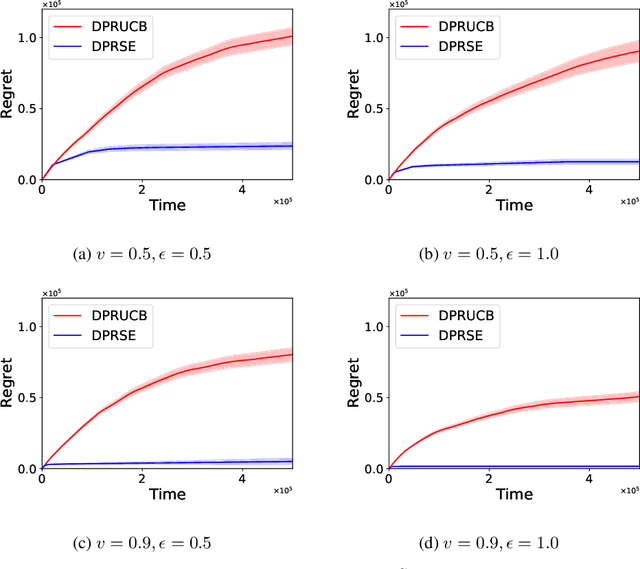
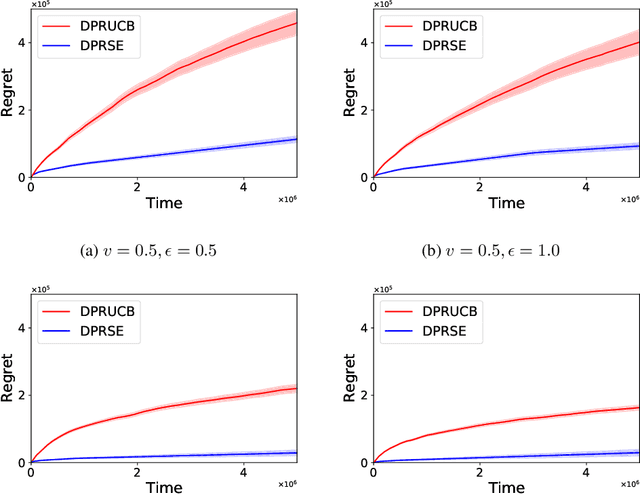
Abstract:In this paper we study the problem of stochastic multi-armed bandits (MAB) in the (local) differential privacy (DP/LDP) model. Unlike the previous results which need to assume bounded reward distributions, here we mainly focus on the case the reward distribution of each arm only has $(1+v)$-th moment with some $v\in (0, 1]$. In the first part, we study the problem in the central $\epsilon$-DP model. We first provide a near-optimal result by developing a private and robust Upper Confidence Bound (UCB) algorithm. Then, we improve the result via a private and robust version of the Successive Elimination (SE) algorithm. Finally, we show that the instance-dependent regret bound of our improved algorithm is optimal by showing its lower bound. In the second part of the paper, we study the problem in the $\epsilon$-LDP model. We propose an algorithm which could be seen as locally private and robust version of the SE algorithm, and show it could achieve (near) optimal rates for both instance-dependent and instance-independent regrets. All of the above results can also reveal the differences between the problem of private MAB with bounded rewards and heavy-tailed rewards. To achieve these (near) optimal rates, we develop several new hard instances and private robust estimators as byproducts, which might could be used to other related problems. Finally, experimental results also support our theoretical analysis and show the effectiveness of our algorithms.
A Distributed Privacy-Preserving Learning Dynamics in General Social Networks
Nov 15, 2020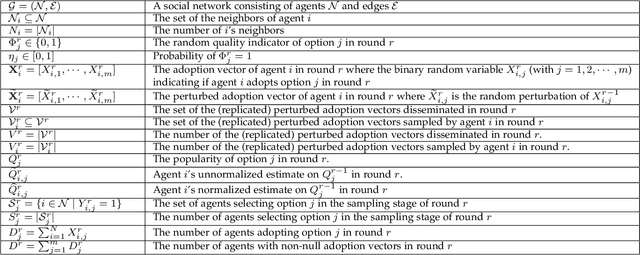
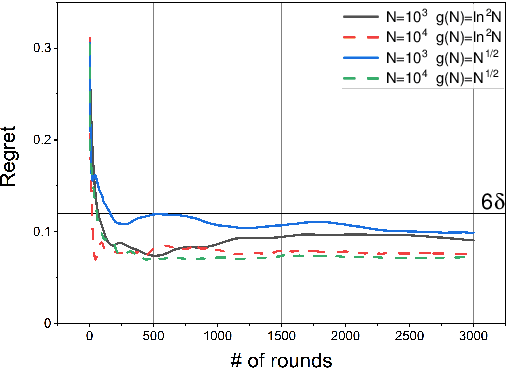
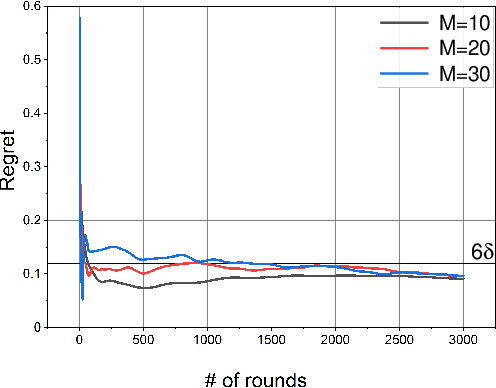
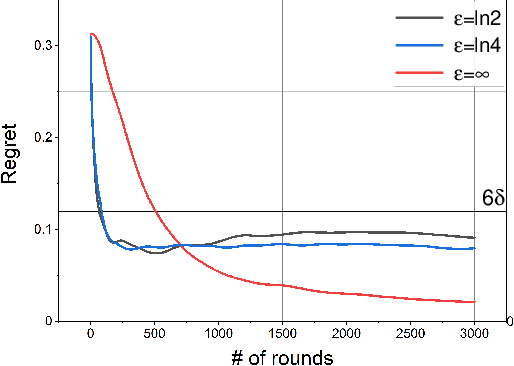
Abstract:In this paper, we study a distributed privacy-preserving learning problem in general social networks. Specifically, we consider a very general problem setting where the agents in a given multi-hop social network are required to make sequential decisions to choose among a set of options featured by unknown stochastic quality signals. Each agent is allowed to interact with its peers through multi-hop communications but with its privacy preserved. To serve the above goals, we propose a four-staged distributed social learning algorithm. In a nutshell, our algorithm proceeds iteratively, and in every round, each agent i) randomly perturbs its adoption for privacy-preserving purpose, ii) disseminates the perturbed adoption over the social network in a nearly uniform manner through random walking, iii) selects an option by referring to its peers' perturbed latest adoptions, and iv) decides whether or not to adopt the selected option according to its latest quality signal. By our solid theoretical analysis, we provide answers to two fundamental algorithmic questions about the performance of our four-staged algorithm: on one hand, we illustrate the convergence of our algorithm when there are a sufficient number of agents in the social network, each of which are with incomplete and perturbed knowledge as input; on the other hand, we reveal the quantitative trade-off between the privacy loss and the communication overhead towards the convergence. We also perform extensive simulations to validate our theoretical analysis and to verify the efficacy of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge