A Distributed Privacy-Preserving Learning Dynamics in General Social Networks
Paper and Code
Nov 15, 2020
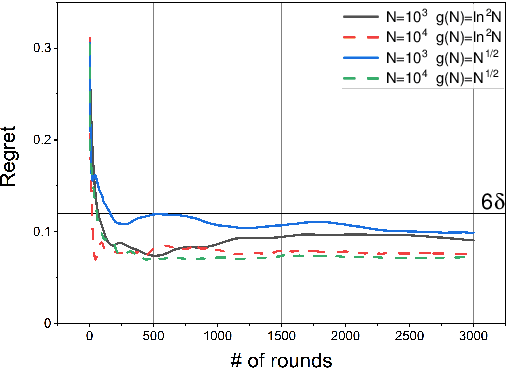
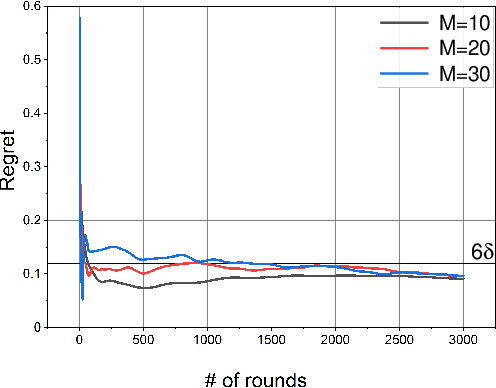
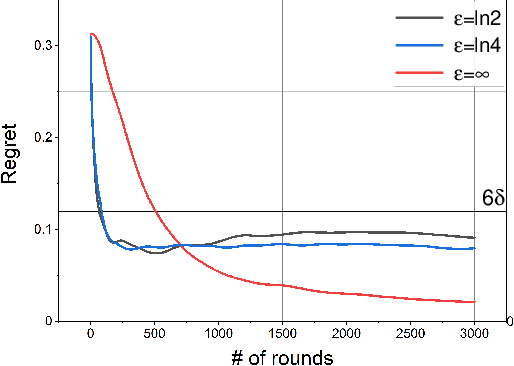
In this paper, we study a distributed privacy-preserving learning problem in general social networks. Specifically, we consider a very general problem setting where the agents in a given multi-hop social network are required to make sequential decisions to choose among a set of options featured by unknown stochastic quality signals. Each agent is allowed to interact with its peers through multi-hop communications but with its privacy preserved. To serve the above goals, we propose a four-staged distributed social learning algorithm. In a nutshell, our algorithm proceeds iteratively, and in every round, each agent i) randomly perturbs its adoption for privacy-preserving purpose, ii) disseminates the perturbed adoption over the social network in a nearly uniform manner through random walking, iii) selects an option by referring to its peers' perturbed latest adoptions, and iv) decides whether or not to adopt the selected option according to its latest quality signal. By our solid theoretical analysis, we provide answers to two fundamental algorithmic questions about the performance of our four-staged algorithm: on one hand, we illustrate the convergence of our algorithm when there are a sufficient number of agents in the social network, each of which are with incomplete and perturbed knowledge as input; on the other hand, we reveal the quantitative trade-off between the privacy loss and the communication overhead towards the convergence. We also perform extensive simulations to validate our theoretical analysis and to verify the efficacy of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge