Distance-Preserving Embeddings in Inhomogeneous Random Graphs

Graph machine learning provides powerful tools for understanding complex networks and learning meaningful node representations. A central challenge, however, is designing embeddings with minimal distortion of both local and global functionals, such as shortest path lengths. Prior distortion guarantees for distance-preserving embeddings are worst-case in nature, producing overly pessimistic bounds that fail to capture the structure of typical large-scale networks. To address this, we analyze shortest-path approximation via landmark-based embeddings on inhomogeneous random graphs, a general model with type-dependent edge probabilities. By retaining shortest paths to a small set of reference nodes called landmarks, landmark-based methods effectively function as virtual graph spanners, where structural heterogeneity and controlled neighborhood expansion modeled via multi-type branching processes enable significantly tighter dimension-distortion trade-offs than classical worst-case bounds. We extend these guarantees to global, component-wide averages and unify the analysis across finite-type and continuous latent spaces through a novel metric sandwiching framework, establishing universal distortion bounds for general $L^2$ kernel models, including heavy-tailed and power-law networks. Finally, we introduce a GNN-augmented variant that replaces rigid, computationally expensive exact shortest-path queries with flexible, structure-aware neural surrogates. By leveraging the inherent alignment between graph neural message-passing and the dynamic programming principles of shortest-path algorithms, our approach demonstrates that models trained on small-scale random graphs learn to extract universal distance-preserving features, achieving robust generalization to large-scale, real-world networks that match or exceed the fidelity of classical, exact landmark-based embeddings.

Local Distance-Preserving Node Embeddings and Their Performance on Random Graphs

Learning node representations is a fundamental problem in graph machine learning. While existing embedding methods effectively preserve local similarity measures, they often fail to capture global functions like graph distances. Inspired by Bourgain's seminal work on Hilbert space embeddings of metric spaces (1985), we study the performance of local distance-preserving node embeddings. Known as landmark-based algorithms, these embeddings approximate pairwise distances by computing shortest paths from a small subset of reference nodes (i.e., landmarks). Our main theoretical contribution shows that random graphs, such as Erd\H{o}s-R\'enyi random graphs, require lower dimensions in landmark-based embeddings compared to worst-case graphs. Empirically, we demonstrate that the GNN-based approximations for the distances to landmarks generalize well to larger networks, offering a scalable alternative for graph representation learning.

Spectral Algorithms Optimally Recover (Censored) Planted Dense Subgraphs

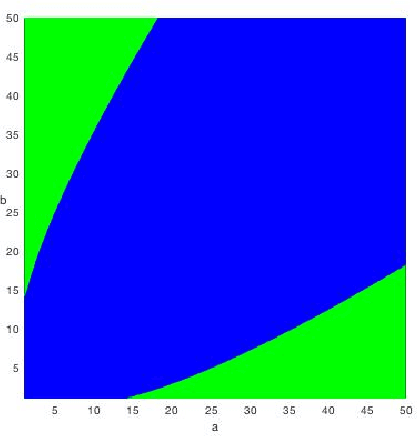
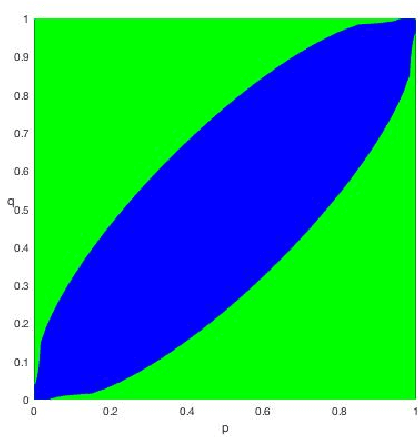
We study spectral algorithms for the planted dense subgraph problem (PDS), as well as for a censored variant (CPDS) of PDS, where the edge statuses are missing at random. More precisely, in the PDS model, we consider $n$ vertices and a random subset of vertices $S^{\star}$ of size $\Omega(n)$, such that two vertices share an edge with probability $p$ if both of them are in $S^{\star}$, and all other edges are present with probability $q$, independently. The goal is to recover $S^{\star}$ from one observation of the network. In the CPDS model, edge statuses are revealed with probability $\frac{t \log n}{n}$. For the PDS model, we show that a simple spectral algorithm based on the top two eigenvectors of the adjacency matrix can recover $S^{\star}$ up to the information theoretic threshold. Prior work by Hajek, Wu and Xu required a less efficient SDP based algorithm to recover $S^{\star}$ up to the information theoretic threshold. For the CDPS model, we obtain the information theoretic limit for the recovery problem, and further show that a spectral algorithm based on a special matrix called the signed adjacency matrix recovers $S^{\star}$ up to the information theoretic threshold.

Community detection using low-dimensional network embedding algorithms

With the increasing relevance of large networks in important areas such as the study of contact networks for spread of disease, or social networks for their impact on geopolitics, it has become necessary to study machine learning tools that are scalable to very large networks, often containing millions of nodes. One major class of such scalable algorithms is known as network representation learning or network embedding. These algorithms try to learn representations of network functionals (e.g.~nodes) by first running multiple random walks and then using the number of co-occurrences of each pair of nodes in observed random walk segments to obtain a low-dimensional representation of nodes on some Euclidean space. The aim of this paper is to rigorously understand the performance of two major algorithms, DeepWalk and node2vec, in recovering communities for canonical network models with ground truth communities. Depending on the sparsity of the graph, we find the length of the random walk segments required such that the corresponding observed co-occurrence window is able to perform almost exact recovery of the underlying community assignments. We prove that, given some fixed co-occurrence window, node2vec using random walks with a low non-backtracking probability can succeed for much sparser networks compared to DeepWalk using simple random walks. Moreover, if the sparsity parameter is low, we provide evidence that these algorithms might not succeed in almost exact recovery. The analysis requires developing general tools for path counting on random networks having an underlying low-rank structure, which are of independent interest.