Community Detection in the Hypergraph SBM: Optimal Recovery Given the Similarity Matrix
Paper and Code
Aug 23, 2022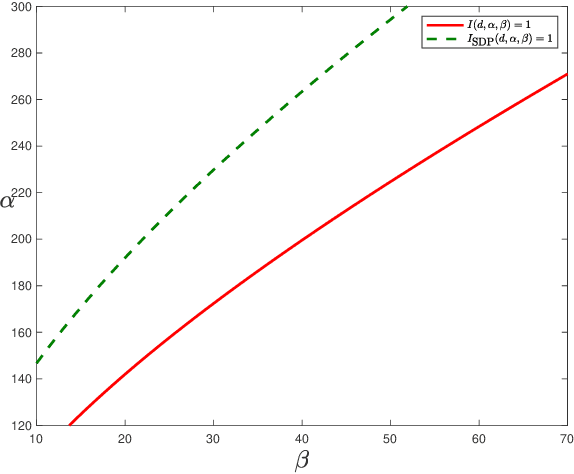
Community detection is a fundamental problem in network science. In this paper, we consider community detection in hypergraphs drawn from the $hypergraph$ $stochastic$ $block$ $model$ (HSBM), with a focus on exact community recovery. We study the performance of polynomial-time algorithms for community detection in a case where the full hypergraph is unknown. Instead, we are provided a $similarity$ $matrix$ $W$, where $W_{ij}$ reports the number of hyperedges containing both $i$ and $j$. Under this information model, Kim, Bandeira, and Goemans [KBG18] determined the information-theoretic threshold for exact recovery, and proposed a semidefinite programming relaxation which they conjectured to be optimal. In this paper, we confirm this conjecture. We also show that a simple, highly efficient spectral algorithm is optimal, establishing the spectral algorithm as the method of choice. Our analysis of the spectral algorithm crucially relies on strong $entrywise$ bounds on the eigenvectors of $W$. Our bounds are inspired by the work of Abbe, Fan, Wang, and Zhong [AFWZ20], who developed entrywise bounds for eigenvectors of symmetric matrices with independent entries. Despite the complex dependency structure in similarity matrices, we prove similar entrywise guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge